|
一、选择题（每题3分，共45分）
1．哪位科学家第一次对天体做圆周运动产生了怀疑？（ ）
A．布鲁诺
B．伽利略
C．开普勒
D．第谷
2．做曲线运动的物体，下列物理量中肯定发生变化的是（ ）
A．速率
B．速度
C．加速度
D．所受合外力
3．在同一高度同一时刻，A球被水平抛出，B球自由下落。以A或B为参照系观察对方，则下列说法中正确的是（ ）
A．以A为参照系看B球，B球做平抛运动
B．以B为参照系看A球，A球做平抛运动
C．以A为参照系看B球，B球沿水平方向做匀速直线运动
D．以B为参照系看A球，A球沿水平方向做匀速直线运动
4．两艘质量各为1×107kg的轮船相距100m时，它们二者之间的万有引力相当于（ ）
A．一个人的重量级
B．一只鸡蛋的重量级
C．一个西瓜的重量级
D．一头牛的重量级
5．正常走动的钟表，其时针和分针都在做匀速转动，下列关系中正确的有（ ）
A．时针和分针角速度相同
B．分针的角速度是时针角速度的12倍
C．时针和分针的周期相同
D．分针的周期是时针周期的12倍
6．某人站在一星球上，以速度v0竖直向上抛一小球，经t秒后，球落回手中，已知该星球半径为R，现将此球沿此星球表面将小球水平抛出，欲使其不落回星球，则抛出时的速度至少为（ ）
A．
B．
C．
D．
7．以速度水平v0抛出一球，某时刻其竖直分位移与水平位移相等，以下判断错误的是（ ）
A．竖直分速度等于水平分速度
B．此时球的速度大小为 v0
C．运动的时间为
D．运动的位移是
8．下列说法正确的是（ ）
A．天王星是人们依据万有引力定律计算的轨道后发现的
B．天王星的运动轨道偏离根据万有引力定律计算出来的轨道，其原因是由于天王星受到轨道外面其它行星的引力作用
C．海王星是应用万有引力定律计算出的它的轨道后发现的
D．冥王星是应用万有引力定律计算出的它的轨道后发现的
9．关于万有引力和万有引力定律的理解错误的是（ ）
A．不能看作质点的两物体间不存在相互作用的引力
B．只有能看作质点的两物体间的引力才能用 计算
C．由知，两物体间距离r减小时，它们之间的引力增大
D．万有引力常量的大小首先是由牛顿测出来的，且等于6．67×10-11N·m2/kg2
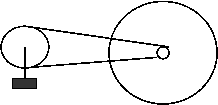
10．如图所示某变速自行车有六个飞轮和三个链轮，链轮和飞轮的齿数如下表所示，前后轮直径为66cm，人骑自行车的速度为4m/s，脚踩踏板做匀速圆周运动的角速度最小值约为（ ）
|
名称 |
链 轮 |
飞 轮 |
|
齿数 |
48 |
35 |
28 |
15 |
16 |
18 |
21 |
24 |
28 |
A．1．9rad/s
B．3．8rad/s
C．6．5rad/s
D．7．1rad/s
11．如图所示，一物体在水平恒力作用下沿水平光滑平面做曲线运动，当从M点运动到N点时，其速度方向恰好改变了90度，则物体在M点到N点的运动过程中，运动的速率（ ）
A．不断变大
B．不断变小
C．先变大再变小
D．先变小再变大
12．已知下面的哪组数据，可以计算出地球的质量M（只知引力常量G）（ ）
A．地球表面的重力加速g和地球的半径R
B．月球绕地球运动的周期T1及月球到地球中心的距离R1
C．地球绕太阳运动的周期T2及地球到太阳中心的距离R2
D．地球“同步卫星”离地面的高度h
13．a、b、c是环绕地球圆形轨道上运行的3颗人造卫星，它们的质量关系是ma＝mb<mc，则（ ）
A．b、c的线速度大小相等，且大于a的线速度
B．b、c的周期相等，且小于a的周期
C．b、c的向心加速度大小相等，且大于a的向心加速度
D．b所需向心力最小
14．一汽车匀速通过半径为R的圆弧形路面，关于汽车的受力情况，正确的是（ ）
A．汽车对路面的压力不变，总等于汽车的重力
B．汽车对路面的压力不断发生变化，总小于汽车所受的重力
C．汽车的牵引力不发生变化
D．汽车的牵引力逐渐变小
15．将完全相同的两小球用长为0．8米的线挂于车的顶部，两球与前后壁接触，由于某种原因，车突然停止运动，此时两线拉力之比为（ ）
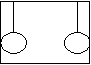
A．1：1
B．1：2
C．1：3
D．1：4
二、填空题（每题6分，共18分）
16．某人乘船横渡一条河，船在静水中的速度与水速一定，且船速大于水速，此人过河的最短时间为T1，若此船用最短位移过河，则需时间T2，则船速与水速之比为__________。
17．已知地球赤道的半径为R，地球自转的周期为T，地球表面的重力加速度为g，则赤道上的物体由于地球自转而产生的加速度为_____________，在圆形轨道上运动的质量为m的人造卫星，它到地面的距离等于地球半径R，则卫星运动的周期为_____________。
18．用m表示地球同步卫星的质量，h表示它离开地面的高度， 表示地球半径， 表地球表面附近的重力加速度， 表示地球自转角速度，则同步卫星受到地球的万有引力大小为_________________或_________________或_________________。
三、计算题（共37分）
19．（7分）在一次“飞车过黄河”的表演中，汽车在空中飞经最高点后在对岸着地。已知汽车从最高点至着地点经历时间约为0．8s，两点间的水平距离约为30m，忽略空气阻力，则汽车在最高点时的速度约为多少？
20．（10分）地球质量为M，半径为R，万有引力恒量为G，发射一颗绕地球表面附近做圆周运动的人造卫星，卫星的速度称为第一宇宙速度。
（1）试推导由上述各量表达的第一宇宙速度的计算式，要求写出推导依据。
（2）若已知第一宇宙速度的大小为v＝7．9km/s，地球半径R＝6．4×106m，万有引力恒量G＝6．67×10-11N·m2/kg2，求地球质量（结果要求二位有效数字）。
21．（10分）设某行星绕质量为M的恒星做匀速圆周运动，旋转半径为r，则从理论上讲旋转周期T0是什么？实测周期T<T0，对此，天文界的共识是星际空间存着在暗物质。设想星际空间的暗物质均匀分布，且理论上可以证明，以恒星M为中心，r为半径的球体以外的均匀分布的暗物质对该行星的运动无影响。试讨论星际暗物质的密度ρ是什么？
22．（10分）两颗卫星在同一轨道平面内绕地球做绕向相同的匀速圆周运动，设地球平均半径为R，a卫星离地高度为0．5R，b卫星离地高度为5R，若某时刻两卫星正好同时通过地面同一点的正上方开始，两卫星第一次出现最远距离的时间是a卫星周期的几倍？
|
