|
运动快慢的描述、速度典型例题
[例1] 一列火车沿平直轨道运行,先以10m/s的速度匀速行驶15min,随即改以15m/s的速度匀速行驶10min,最后在5min内又前进1000m而停止.则该火车在前25min及整个30min内的平均速度各为多大?它通过最后2000m的平均速度是多大?
[分析] 根据匀速直线运动的规律,算出所求时间内的位移或通过所求位移需要的时间,即可由平均速度公式算出平均速度.
[解答] 火车在开始的15min和接着的10min内的位移分别为:
s1=v1t1=10×15×60m=9×103m
s2=v2t2=15×10×60m=9×103m
所以火车在前25min和整个30min内的平均速度分别为:

因火车通过最后2000m的前一半位移以v2=15m/s匀速运动,经历时间为:
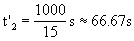
所以最后2000m内的平均速度为:
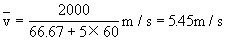
[说明]由计算可知,变速运动的物体在不同时间内(或不同位移上)的平均速度一般都不相等.
[例2]某物体的位移图象如图所示.若规定向东为位移的正方向,试求:物体在OA、AB、BC、CD、DE各阶段的速度.

[分析]物体在t=0开始从原点出发东行作匀速直线运动,历时2s;接着的第3s~5s内静止;第6s内继续向东作匀速直线运动;第7s~8s匀速反向西行,至第8s末回到出发点;在第9s~ 12s内从原点西行作匀速直线运动.
[解]由s-t图得各阶段的速度如下:

AB段:v2=0;
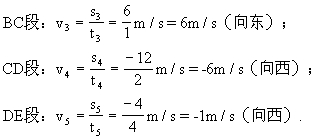
[说明] 从图中可知,经t=12s后,物体位于原点向西4m处,即在这12s内物体的位移为-4m.而在这12s内物体的路程为(12 12 4)m=28m.由此可见,物体不是作单向匀速直线运动时,位移的大小与路程不等.
[例3] 图1所示为四个运动物体的位移图象,试比较它们的运动情况.
[分析]这四个物体的位移图象都是直线,其位移又都随时间增加,说明都向着同方向(位移的正方向)作匀速直线运动,只是其速度的大小和起始情况不同.
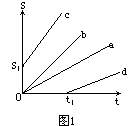
[答]a、b两物体从t=0开始,由原点出发向正方向作匀速直线运动.c物体在t=0时从位于原点前方s1处向正方向作匀速直线运动.d物体在时间t1才开始向正方向作匀速直线运动.由图中可知,任取相同时间△t,它们的位移△s大小不同:△Sc>△SB>△Sa>△Sd,所以它们的速度大小关系为vc>vB>va>vd.
[说明]这四条图线所对应的物体的运动,可以想象为四个百米赛跑的运动员.发令枪响,a、b两运动员从起跑线上以不同速度匀速出发.c运动员则“抢跑”——在发令枪响前t0时刻已开始出发,因此在发令枪响时刻(t=0)已跑到正前方s1处.d运动员则反应迟缓,发令枪响后经一段时间t1才开始出发——相当于在发令枪响时(t=0)从位于起跑线后s0处出发的(图2).
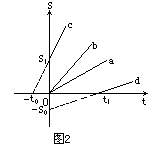
根据图线斜率的意义可知,匀速直线运动位移图象斜率的大小等于速度,即
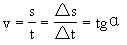
[例4] 对于作匀速直线运动的物体,则 [ ]
A.任意2s内的位移一定等于1s内位移的2倍
B.任意一段时间内的位移大小一定等于它的路程
C.若两物体的速度相同,则它们的速率必然相同,在相同时间内通过的路程相等
D.若两物体的速率相同,则它们的速度必然相同,在相同时间内的位移相等
[分析] 物体作匀速直线运动时,速度v的大小、方向恒定不变,由公式s=vt知,其位移与时间成正比.又由于速度v方向不变,其轨迹是一条单向的直线,任意时间内的位移大小与路程相等.当v1=v2时,表示两者的大小、方向都相同,相同时间内的路程必相等.但当速率|v1|=|v2|时,两物体的运动方向可能不同,相同时间内的位移可以不等.
[答] A、B、C.
[例5]甲、乙、丙三个物体运动的 S—t图象如图所示,下列说法中正确的是 [ ]

A.丙物体作加速直线运动
B.甲物体作曲线运动
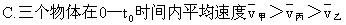

[误解]选(B),(C),(D)。
[正确解答] 选(A)。
[错因分析与解题指导] 物体运动的位移图象(简称S—t图)表示作直线运动物体的位移随时间的变化规律,位移图象不是物体的运动轨迹。选项(B)把图线误认为是物体的运动轨迹,是完全错误的。
位移图象中图线的斜率表示物体运动速度的大小,故选项(A)正确。
平均速度=位移/时间,0—t0 时间内三物体有相同的位移,故应有 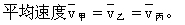
平均速率=路程/时间,0—t0时间内乙、丙两物体路程相等,而甲物体运动路程大,
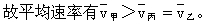
[例6]甲乙两车沿平直公路通过同样的位移,甲车在前半段位移上以v1=40km/h的速度运动,后半段位移上以v2=60km/h的速度运动;乙车在前半段时间内以v1=40km/h的速度运动,后半段时间以v2=60km/h的速度运动,则甲、乙两车在整个位移中的平均速度大小的关系是 [ ]

[分析] 设总位移为s,则甲车运动时间为
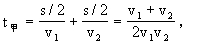
所以甲车的平均速度
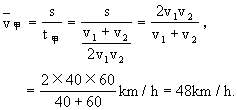
设乙车运动总时间为t乙,则乙车的总位移为
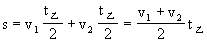
所以乙车的平均速度
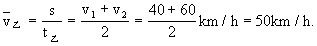
[答] C.
 计算,它不等于速度的平均在变速直线运动中,若物体运动的前一半时间平均速度为v1,后一 计算,它不等于速度的平均在变速直线运动中,若物体运动的前一半时间平均速度为v1,后一  求出。若运动的前一半位移平均速度为v1,后一半位移的平均速度为v2,则全程的平 求出。若运动的前一半位移平均速度为v1,后一半位移的平均速度为v2,则全程的平
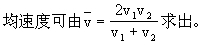
[例7]列车进站前先关闭汽阀,当它匀减速滑行300m时,列车的速度已经减半,以后又继续滑行20s后恰好停于站台上.求列车滑行的总位移和最后10s内的位移.
[分析] 这里的研究对象是列车,根据题意作出的运动示意图如图所示.
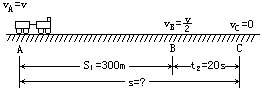
设列车行至A处开始刹车滑行的速度为v,至B处速度为 
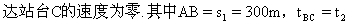 =20s. =20s.
[解] 因vB 恰等于整个滑行过程中的平均速度,即
vB = 
 车在AB段和BC段的运动时间必定相等,即 车在AB段和BC段的运动时间必定相等,即
t1=t2=20s
因列车在AB段和BC段的平均速度分别为

即
v1∶v2=3∶1,

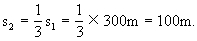

假如从终点C逆着原列车运动方向考虑,列车做的是初速为零的匀加速运动.根据s∝t2的关系,最后10s(即逆向观察时的第1个10s)内的位移仅为最后20s(即逆向观察时最初两个10s)内位移的1/4,故
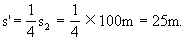
[说明] 本题由于灵活应用了“时间中点”的速度特点、位移的比例关系和逆向转换的思考方法,得以能较迅速的求解,请读者予以体会.
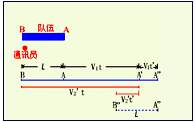
[例8] 一列队伍长L=120m,行进速度v1=1.6m/s.为了传达一个命令,通讯员从队伍排尾跑步赶到队伍排头,其速度v2=3m/s,然后又立即用与队伍行进速度相同大小的速度返回排尾.问:
(1)通讯员从离开队伍到重又回到排尾共需多少时间?
(2)通讯员归队处与离队处相距多远?
[分析]这里有两个研究对象:通讯员和行进中的队伍,两者都作匀速直线运动,其运动示意图如图所示.设队伍原位置为AB,通讯员从排尾赶到排头时,排头已到位置A',所用时间为t,通讯员返回排尾时,排头的位置为A″,所用时间为t′.在时间t内,通讯员与队伍位移之差等于L;在时间t′内, 通讯员与队伍位移大小之和等于L.
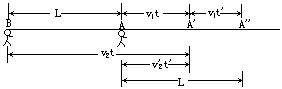
[解](1)通讯员从排尾赶到排头时,有关系式:
v2t-v1t=L ①
设通讯员从排头返回排尾的速度为v2′,其值为v2′=v1= 1.6m/s,又有关系式:
v1t' v'2t'=2v1t'=L ②
联立两式,得通讯员从离开队伍(排尾)到重新返回排尾共需时间:

(2)通讯员归队处与离队处相隔距离就是整个队伍在同样时间内行进的距离,即
s'=v1T=1.6×123.2m=197.1m
[说明] 根据运动的相对性,假如把行进中的队伍作为参照物,就可以简化为一个研究对象,即通讯员相对于“静止”队伍的匀速直线运动.离队时,通讯员以大小等于(v2-v1)的速度向排头做匀速运动,赶
 到归队的时间: 到归队的时间:
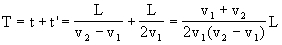
|