机械运动、位移典型例题

　　[例1] 甲、乙、丙三架观光电梯，甲中乘客看一高楼在向下运动；乙中乘客看甲在向下运动；丙中乘客看甲、乙都在向上运动.这三架电梯相对地面的运动情况是 [　　 ]

　　A.甲向上、乙向下、丙不动

　　B.甲向上、乙向上、丙不动

　　C.甲向上、乙向上、丙向下

　　D.甲向上、乙向上、丙也向上，但比甲、乙都慢

　　[分析] 电梯中的乘客观看其他物体的运动情况时，是以自己所乘的电梯为参照物.甲中乘客看高楼向下运动，说明甲相对于地面一定在向上运动.同理，乙相对甲在向上运动，说明乙对地面也是向上运动，且运动得比甲更快.丙电梯无论是静止，还是在向下运动，或以比甲、乙都慢的速度在向上运动，丙中乘客看甲、乙两电梯都会感到是在向上运动.

　　[答] B、C、D.

　　[例2] 下列关于质点的说法中，正确的是 [　　 ]

　　A.体积很小的物体都可看成质点

　　B.质量很小的物体都可看成质点

　　C.不论物体的质量多大，只要物体的尺寸跟物体间距相比甚小时，就可以看成质点

　　D.只有低速运动的物体才可看成质点，高速运动的物体不可看作质点

　　[分析] 一个实际物体能否看成质点，跟它体积的绝对大小、质量的多少以及运动速度的高低无关，决定于物体的尺寸与物体间距相比的相对大小.例如，地球可称得上是个庞然大物，其直径约为1.28×107 m，质量达到6×1024kg，在太空中绕太阳运动的速度每秒几百米.由于其直径与地球离太阳的距离（约1.5×1011m）相比甚小，因此在研究地球的公转运动时，完全可以忽略地球的外形、大小及地球自身的运动，把它看成一个质点.

　　[答] C.

　　[例3]下列各种情况，可以把研究对象（黑体者）看作质点的是 [　　 ]

　　A. 研究小木块的翻倒过程

　　B. 讨论地球的公转

　　C. 解释微粒的布朗运动

　　D. 计算整列列车通过某一路标的时间

　　[误解一] 小木块体积小，远看可视为一点；作布朗运动的微粒体积极小，当然是质点，故选（A）、（C）。

　　[误解二] 列车作平动，车上各点运动规律相同，可视为质点，故选（D）。

　　[正确解答] 讨论地球的公转时，地球的直径（约1.3×104km）和公转的轨道半径（约1.5×108km）相比要小得多，因而地球上各点相对于太阳的运动差别极小，即地球的大小和外形可以忽略不计，可把地球视为质点，故选（B）。

　　[错因分析与解题指导] 物理研究中常建立起一些理想化的模型，它是物理学对实际问题的简化，也叫科学抽象。它撇开与当前观察无关的因素和对当前考察影响很小的次要因素，抓住与考察有关的主要因素进行研究、分析、解决问题，质点就是一个理想化的模型。[误解一] 以为质点是指一个很小的点。但在小木块的翻倒过程中，木块各点绕一固定点转动，各点运动情况不同，不可看作质点。至于作布朗运动的粒子，尽管体积极小，仍受到来自各个方向上的液体分子（具有更小体积）的撞击，正是这种撞击作用的不平衡性使之作无规则运动，也不可把布朗运动粒子视为质点。[误解二]以为火车在铁道上的运动为平动，可视为质点。而本题实际考察的是经过某路标的时间，就不能不考察它的长度，在这情况中不能视其为质点。

　　[例4]关于质点的位移和路程的下列说法中正确的是 [　　 ]

　　A. 位移是矢量，位移的方向即质点运动的方向

　　B. 路程是标量，即位移的大小

　　C. 质点沿直线向某一方向运动，通过的路程等于位移的大小

　　D. 物体通过的路程不等，位移可能相同

　　[误解]选（A），（B）。

　　[正确解答] 选（C），（D）。

　　[错因分析与解题指导] 位移是表示物体位置变化的物理量，它是矢量，其方向由质点初位置指向末位置，其大小是连接质点始、末位置线段的长度。路程是指质点所通过的实际轨迹的长度，它只有大小，没有方向，是标量。

　　例如，质点原来在 A点，经过一段时间沿轨迹 ACB运动到 B点，有

　　在曲线运动中，位移大小不等于路程，即使在直线运动中，位移的大小也不一定等于路程。如图2所示，物体从初位置 A经过B运动到C， ，而路程是AC CB。事实上，只有做直线运动的质点始终向着同一个方向运动时，位移的大小才等于路程。

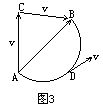
　　位移的方向是由质点的始位置指向末位置的特定方向，通常它不是质点的运动方向。图3表示质点由始位置A分别沿折线ACB和曲线 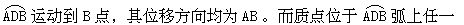位置D时的运动方向，以及作折线运动时的运动方向均如图中所示，它 同路径由A运动到B，质点的位移是相同的。

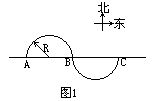
　　[例5] 一个质点沿两个半径为R的半圆弧由A运动到C（如图1），则它的位移和路程分别为 [　　 ]

　　A. 4R，2πR

　　B. 4R向东，2πR向东

　　C. 4πR向东，4R

　　D. 4R向东，2πR

　　[分析] 位移大小等于 AC，方向由A指向C；路程等于沿两个半圆计算的弧长，无方向.

　　[答]D.

　　[说明]质点作直线运动时，位移（s）可以用末位置的坐标（x）和初位置的坐标（x0）表示：S=x-x0，如图2所示。取向右方向为x轴正方向，O为原点，则质点从A（xA=2m）运动到B（xB=4m）和从A运动到C（xC= -5m）的位移可表示为：

　　SAB=xB-xA=4m-2m=2m（向右）

　　SAC=xC-xA=-5m-2m=-7m（向左）