牛顿运动定律·例题分析

例1　 一向右运动的车厢顶上悬挂两单摆M与N，它们只能在如图3-1所示平面内摆动．某一瞬时出现如图3-1所示情景，由此可知车厢的运动及两单摆相对车厢运动的可能情况是 [　　　 ]

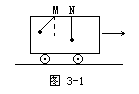
A．车厢作匀速直线运动，M摆动，N静止

B．车厢作匀速直线运动，M摆动，N也摆动

C．车厢作匀速直线运动，M静止，N摆动

D．车厢作匀加速直线运动，M静止，N也静止

分析　 作用在两个摆上的力只有摆的重力和摆线张力．

当车厢作匀速直线运动时，N摆相对车厢静止或摆动中经过平衡位置的瞬间，此时摆所受重力和摆线张力在同一竖直线上，可以出现如图3-1中所示情景．M摆所受重力和摆线张力不在一直线上，不可能静止在图中所示位置，但可以是摆动中达到极端位置（最大偏角的位置）的瞬间．A、B正确，C错．

当车厢作匀加速直线运动，作用在摆球上的重力和摆线张力不再平衡，它们不可能在一直线上，其合力使摆球产生水平方向的加速度．所以，M静止在图中位置是可能的，但N也静止不可能，D错．

答A、B．

说明　 M摆静止在图3-1中情景，要求摆球所受重力和摆线张力的合力F=mg·tgα=ma，因此车厢的加速度与摆线偏角间必须满足关系（图3-2），即

a=gtgα．

例2　 电梯地板上有一个质量为200kg的物体，它对地板的压力随时间变化的图像如图3-3所示．则电梯从静止开始向上运动，在7s内上升的高度为多少？

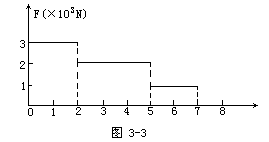
分析　 以物体为研究对象，在运动过程中只可能受到两个力的作用：重力mg=2000N，地板支持力F．在t=0-2s内，F＞mg，电梯加速上升，t=2-5s内，F=mg，电梯匀速上升，t=5-7s内，F＜mg，电梯减速上升．

解 　若以向上的方向为正方向，由上面的分析可知，在t=0-2s内电梯的加速度和上升高度分别为

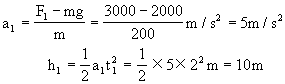
电梯在t=2s时的速度为

v=a1t1=5×2m／s=10m／s，

因此，t=2-5s内电梯匀速上升的高度为

h2=vt2=10×3m=30m．

电梯在t=5-7s内的加速度为

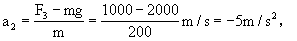
即电梯作匀减速上升，在t=5-7s内上升的高度为

所以，电梯在7s内上升的总高度为

h=h1 h2 h3

=（10 30 10）m

=50m．

例3　 为了安全，在公路上行驶的汽车之间应保持必要的距离．已知某高速公路的最高限速 v=120km／h，假设前方车辆忽然停下，后车司机从发现这一情况，经操纵刹车，到汽车开始减速所经历的时间（即反应时间）t=0.50s．刹车时汽车受到阻力的大小f为汽车重力的0.40倍，该高速公路上汽车间的距离s至少应为多少？取 g=10m／s2．

分析　 后车在司机的反应时间前、后看作两种不同的运动，这两种运动的位移之和即为两车距离的最小值．

解　 在司机的反应时间内，后车作匀速运动．其位移为

s1=vt．

刹车后，在阻力f作用下匀减速滑行，其加速度大小为

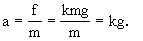
汽车在刹车滑行过程中的位移为

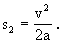
所以，高速公路上两车间距至少应为

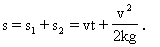
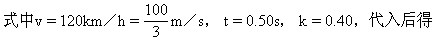
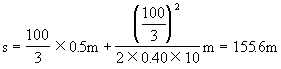
≈160m．

例4　 在升降机地面上固定着一个倾角α=30°的光滑斜面，用一条平行于斜面的细绳拴住一个质量m=2kg的小球（图3-4）．当升降机以加速度a=2m／s2竖直向上匀加速运动时，绳子对球的拉力和小球对斜面的压力分别为多少？

（取g=10m／s2）

分析　 以小球为研究对象，它随升降机向上加速运动过程中受到三个力作用：重力mg、绳子拉力T、斜面支持力N．由于这三个力不在一直线上，可采用正交分解法，然后列出牛顿第二定律方程，即可求解．

解　 根据小球的受力情况（图3-5），把各个力分解到竖直、水平两方向．在竖直方向上（取向上为正方向），根据牛顿第二定律得

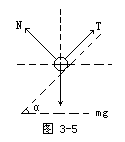
Tsinα Ncosα-mg=ma．　　　　　　　　　　　　　　　 （1）

在水平方向上（取向右为正方向），根据力平衡条件得

Tcosα-Nsinα=0．　　　　　　　　　　　　　　　　　 （2）

将式（1）乘以sinα，式（2）乘以cosα，两式相加得绳子对球的拉力为

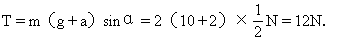
将式（1）乘以cosα，式（2）乘以sinα，两式相减得斜面对球的支持力为

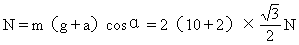
根据牛顿第三定律，球对斜面的压力

N′=-N=-20.8N，

式中“-”号表示N′与N方向相反，即垂直斜面向下．

说明　 本题是已知运动求力，解题中非常全面地体现了应用牛顿第二定律的解题步骤，需注重体会．

需要注重的是，题中求出的N是斜面对球的支持力，还必须用牛顿第三定律，得出球对斜面的压力．

例5　 如图3-6所示，传送带与水平面夹角为θ=37°，以速度v=10m／s匀速运行着．现在传送带的A端轻轻放上一个小物体（可视为质点），已知小物体与传送带之间的摩擦因数μ=0.5，A、B间距离s=16m，则当皮带轮处于下列两情况时，小物体从A端运动到B端的时间分别为多少？

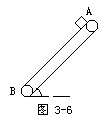
（1）轮子顺时针方向转动；（2）轮子逆时针方向转动．

已知sin37°=0.6，cos37°=0.8，取g=10m／s2．

分析　 小物体从A到B的运动过程中，受到三个力作用：重力mg、皮带支持力N、皮带摩擦力f．由于摩擦力的方向始终与物体相对运动的方向相反，因此当轮子按不同方向转动时．或小物体与皮带的相对运动方向变化时，摩擦力方向都会不同．当判定清楚小物体的受力情况后，根据牛顿第二定律结合运动学公式即可求解．

解　 （1）轮子顺时针方向转动轮子顺时针方向转动时，带动皮带绕轮顺时针方向转动，因此皮带作用于小物体的摩擦力沿皮带向上，物体的受力情况如图3-7所示．

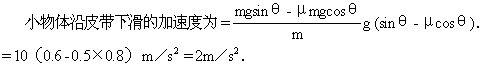
小物体从A端运动到B端的时间t为

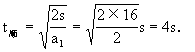
（2）轮子逆时针方向转动轮子逆时针方向转动时，皮带带动小物体下滑，因此皮带作用于小物体的摩擦力沿皮带向下，物体的受力情况如图3-8所示．

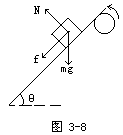
小物体沿皮带下滑的加速度

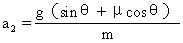
=10（0.6 0.5×0.8）m／s2

=10m／s2．

小物体加速到皮带运行速度 v=10m／s的时间为

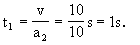
在这段时间内，小物体沿皮带下滑的距离

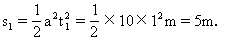
此后，小物体沿皮带继续加速下滑时，它相对于皮带的运动方向向下，因此皮带对小物体的摩擦力沿皮带向上，如图3-9所示．其加速度变为

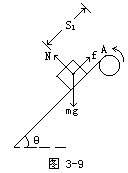
a2=g（sinθ-μcosθ）

=2m／s2．

它从该位置起运动到B端的位移为（s-s1）=16m-5m=11m，由

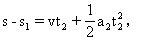
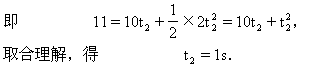
所以小物体从A端运动到B端的时间为

t逆=t1 t2=2s．

说明　 （1）本题求解的要害是根据相对运动方向正确判定摩擦力的方向，同时应注重整个运动中的变化情况．

（2）在前半题中，严格地说，还应先从皮带运行速度测算一下小物体达到该速度的时间，即

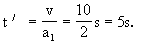
在这5s内小物体匀加速下滑的位移为

可见，小物体从A到B过程中确实始终以加速度a1=2m／s2作匀加速运动．因此其运动时间为
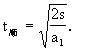