|
曲线运动综合复习
知识要点:
1. 运动的合成和分解
速度的合成和分解一定要依据其实际效果进行,合运动一定是物体的实际运动(换句话说,物体实际运动方向是合速度的方向,即物体实际运动方向是平行四边形对角线的方向)
例题:如图所示,水平面上有一物体,小车通过定滑轮用绳子拉它,在图示位置时,若小车的速度为 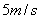 ,则物体的瞬时速度为 m/s。 ,则物体的瞬时速度为 m/s。

解析:由小车的速度为5m/s,小车拉绳的速度 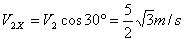 ,则物体受到绳的拉力,拉绳的速度 ,则物体受到绳的拉力,拉绳的速度 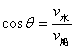 ,则物体的瞬时速度为 ,则物体的瞬时速度为  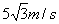 。 。

2. 渡河问题:渡河问题所涉及的就是渡河的最短时间问题和渡河的最短位移问题。
(1)最短时间问题:无论  、 、  ,还是 ,还是  ,只要 ,只要 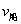 沿垂直与河岸方向渡河,则所用时间最短,此时 沿垂直与河岸方向渡河,则所用时间最短,此时 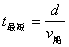 (其中d为河宽) (其中d为河宽)
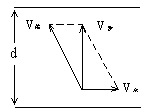
(2)渡河的最短位移问题:
① 当  时, 时, 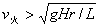 与河岸垂直, 与河岸垂直, 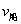 充当斜边 充当斜边  。 。
② 当  时,无最短位移。 时,无最短位移。
③ 当  时,以 时,以 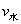 的箭头为圆心,以 的箭头为圆心,以 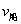 的大小为半径,画弧,以 的大小为半径,画弧,以 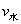 的箭尾为起点做圆弧的切线,延长该切线到对岸,即为最短位移,由三角形相似 的箭尾为起点做圆弧的切线,延长该切线到对岸,即为最短位移,由三角形相似 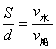 , ,
∴ 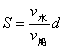 。 。

3. 平抛运动
运动的合成与分解是平抛运动的研究依据,对平抛运动的研究也将进一步提高运用运动的合成方法解决问题的能力。
(1)平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动。这两个分运动同时存在,按各自的规律独立进行,水平初速度的大小不会影响竖直方向的分运动。一般情况下,竖直方向的分运动决定着平抛物体的运动的时间。
(2)平抛运动的轨迹。
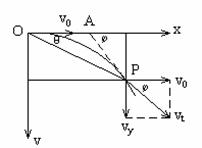
设物体做平抛运动到某点P( 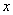 , ,  ),如图所示 ),如图所示
则轨迹方程为 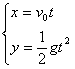 ,消去参数 ,消去参数 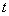 ,得 ,得 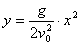 (抛物线)。 (抛物线)。
(3)平抛物体经一段时间,其速度方向和位移方向是不相同的,如图所示。
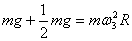 , , 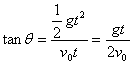 ,即 ,即  。 。
(4)如图所示,曲线上任一点P( 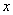 , ,  )的速度方向反向延长线交于 )的速度方向反向延长线交于 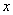 轴上的A点,由图可知 轴上的A点,由图可知 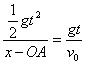 ,所以OA= ,所以OA= 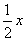 。 。
此结论可应用到类平抛运动中,如带电粒子在匀强电场中偏转。
(5)平抛物体在相同时间内,速度变化量相同,  ,且方向为竖直向下,如图所示。 ,且方向为竖直向下,如图所示。
(6)平抛运动在竖直方向上的分运动是自由落体运动,要充分应用初速度为零的匀加速直线运动的规律解决平抛运动问题。
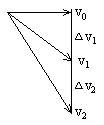 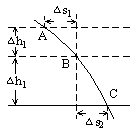
如图所示,实线为某质点平抛运动轨迹的一部分,测得AB、BC间的水平距离 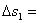 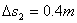 ,高度差 ,高度差  , ,  ,由此可知,质点平抛的初速度 ,由此可知,质点平抛的初速度 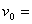 ,抛出点到A点的水平距离为 。(g取10m/s2) ,抛出点到A点的水平距离为 。(g取10m/s2)
由 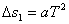 ,可得 ,可得 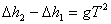 。 。
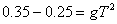 ,∵ ,∵ 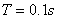 。 。
由  ,∴ ,∴ 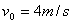 。 。
由初速度为零的匀加速直线运动规律得相等时间内位移之比为   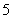 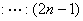 ,可知 ,可知 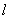 ,故A点不是抛出点,抛出点到A点的时间为2T,A点离抛出点水平距离 ,故A点不是抛出点,抛出点到A点的时间为2T,A点离抛出点水平距离 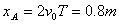 。 。
5描述圆周运动的物理量:
(1)线速度:大小为 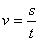 ,方向沿圆弧的切线方向。 ,方向沿圆弧的切线方向。
(2)角速度: 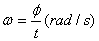
(3)周期T,频率f
作圆周运动的物体运动一周所用的时间叫做周期。
作圆周运动的物体单位时间内绕圆心转过的圈数叫做频率。
(4) 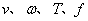 的关系 的关系
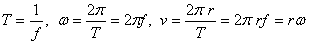
(5)向心加速度:
= 1 \* GB3 ① 物理意义:描述线速度方向改变的快慢。
= 2 \* GB3 ② 大小:  。 。
= 3 \* GB3 ③ 方向:总是指向圆心,与线速度方向垂直。
6. 匀速圆周运动:
(1)定义:做圆周运动的物体,若在相等的时间里通过的圆弧长度相等,就是匀速圆周运动。
(2)运动学特征:线速度大小、向心加速度大小不变,但方向时刻改变,故匀速圆周运动是变速运动。
(3)向心力:
= 1 \* GB3 ① 作用效果:产生向心加速度,以不断改变物体的速度方向,维持物体做圆周运动。
= 2 \* GB3 ② 大小: 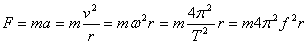 。 。
= 3 \* GB3 ③ 产生:向心力是按效果命名的力,不是某种性质的力。
(4)向心加速度的分析:
向心加速度是向心力的效果,其方向与向心力相同,总是指向圆心。
从运动的角度看,向心加速度是描述做匀速圆周运动的物体的速度方向变化情况的物理量,其计算公式
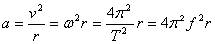 。 。
由上式可以看出:当线速度v一定时,向心加速度a跟轨道半径r成反比;当角速度 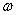 一定时,向心加速度a跟r成正比;由于 一定时,向心加速度a跟r成正比;由于 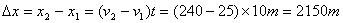 ,所以a总是跟v与 ,所以a总是跟v与 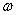 的乘积成正比。 的乘积成正比。
(5)圆周运动中向心力的特点:
= 1 \* GB3 ① 匀速圆周运动:由于匀速圆周运动仅是速度方向变化而速度大小不变,故只存在向心加速度,物体受到外力的合力就是向心力。可见,合外力大小不变,方向始终与速度方向垂直且指向圆心,是物体做匀速圆周运动的条件。
= 2 \* GB3 ② 变速圆周运动:速度大小发生变化,向心加速度和向心力都会相应变化,求物体在某一点受到的向心力时,应使用该点的瞬时速度,在变速圆周运动中,合外力不仅大小随时间改变,其方向也不沿半径指向圆心,合外力沿半径方向的分力提供向心力,使物体产生向心加速度,改变速度的方向,合外力沿轨道切线方向的分力,使物体产生切向加速度,改变速度的大小。
(6)圆周运动中的临界问题:
关于临界问题总是出现在变速圆周运动中,竖直平面内的圆周运动是典型的变速圆周运动,一般情况下,只讨论最高点和最低点的情况:
= 1 \* GB3 ① 如图所示,没有物体支撑的小球,在竖直平面内做圆周运动过最高点的情况:
<1> 临界条件:小球达到最高点时绳子的拉力;(或轨道的弹力)刚好等于零,小球的重力提供其做圆周运动的向心力,即 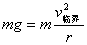 ,上式中的 ,上式中的 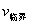 是小球通过最高点的最小速度,通常叫临界速度 是小球通过最高点的最小速度,通常叫临界速度  。 。

<2> 能过最高点的条件: 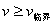 (此时绳、轨道对球分别产生拉力、压力)。 (此时绳、轨道对球分别产生拉力、压力)。
<3> 不能过最高点的条件: 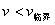 (实际上球还没有到最高点就脱离了轨道)。 (实际上球还没有到最高点就脱离了轨道)。
= 2 \* GB3 ② 如图所示,有物体支撑的小球在竖直平面内做圆周运动过最高点的情况:
<1> 临界条件:由于硬杆和管壁的支撑作用,小球恰能达最高点的临界速度  。 。
<2> 如图所示的小球过最高点时,轻杆对小球的弹性情况:

当  时,轻杆对小球有竖直向上的支持力 时,轻杆对小球有竖直向上的支持力 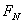 ,其大小等于小球的重力,即 ,其大小等于小球的重力,即  。 。
当  时,杆对小球的作用力的方向竖直向上,大小随速度的增大而减小,其取值范围是: 时,杆对小球的作用力的方向竖直向上,大小随速度的增大而减小,其取值范围是:  。 。
当  时, 时,  。 。
当 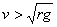 时,杆对小球有指向圆心的拉力,其大小随速度的增大而增大。 时,杆对小球有指向圆心的拉力,其大小随速度的增大而增大。
<3> 如图所示的小球过最高点时,光滑硬管对小球的弹力情况,同上面图(1)的分析。

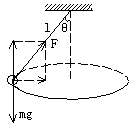
= 3 \* GB3 ③ 圆锥摆的情况:
如图所示,圆锥摆的情况是水平面内的圆周运动情况,将绳的拉力竖直分解与重力平衡,水平分解提供向心力,即:
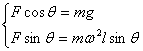 ,∴ ,∴ 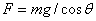 , ,
 ,∴ ,∴ 
由  可以看出 可以看出 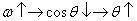 ,反之 ,反之 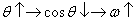
= 4 \* GB3 ④ 火车转弯的情况:
 ∴ ∴ 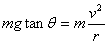
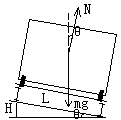
∵  很小 ∴ 很小 ∴ 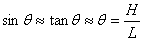
∴ 
∴ 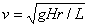
若 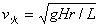 ,则内外轨均无挤压, ,则内外轨均无挤压,  ; ;
若 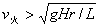 , ,  不足以提供所需的向心力,此时火车向外甩,外侧轮缘挤压外轨,外轨给轮缘一指向圆心方向的弹力,补充向心力 不足以提供所需的向心力,此时火车向外甩,外侧轮缘挤压外轨,外轨给轮缘一指向圆心方向的弹力,补充向心力  ; ;
若 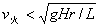 , ,  大于所需要的向心力,此时火车被向里拉,内侧轮缘挤压内轨,内轨给轮缘一远离圆心方向的弹力, 大于所需要的向心力,此时火车被向里拉,内侧轮缘挤压内轨,内轨给轮缘一远离圆心方向的弹力,  。 。
【典型例题分析】
[例1] 甲乙两船在静水中航行速度分别为  、 、  ,两船从同一渡口向河对岸划去,已知甲船以最短时间过河,乙船以最短航程过河,结果两船抵达对岸的地点恰好相同,则甲、乙两船渡河所用时间之比 ,两船从同一渡口向河对岸划去,已知甲船以最短时间过河,乙船以最短航程过河,结果两船抵达对岸的地点恰好相同,则甲、乙两船渡河所用时间之比  为多少? 为多少?
解析:船参与了自身划行和随水漂流两个分运动,由于水流速度并不影响船在垂直河岸方向的分运动,所以当船头垂直指向对岸运动,渡河时间最短 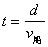 (其中 (其中  为河宽),这时船到达正对岸的下游。 为河宽),这时船到达正对岸的下游。
对于船渡河的最小位移问题又分成两种情况。
(1)若  ,此时最短位移为河宽d,如图所示,船头指向与河岸上游成 ,此时最短位移为河宽d,如图所示,船头指向与河岸上游成  角,满足 角,满足 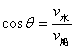 ,渡河时间 ,渡河时间 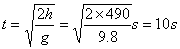 ,船到达正对岸,所以此种情况不符合甲、乙两船抵达对岸的同一地点。 ,船到达正对岸,所以此种情况不符合甲、乙两船抵达对岸的同一地点。

(2)若  ,这种情况,不管如何调整 ,这种情况,不管如何调整 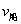 的方向,船的运动方向都不可能沿垂直河岸的方向,当船到达对岸时一定会被水冲向下游,船渡河的实际位移一定大于河宽。当船的速度方向与合速度方向垂直时,船渡河的位移最小,如图所示,由于两船抵达河对岸同一点,说明两船在河水中的合速度方向相同。 的方向,船的运动方向都不可能沿垂直河岸的方向,当船到达对岸时一定会被水冲向下游,船渡河的实际位移一定大于河宽。当船的速度方向与合速度方向垂直时,船渡河的位移最小,如图所示,由于两船抵达河对岸同一点,说明两船在河水中的合速度方向相同。

解法一:
由图可知: 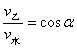 ,① ,①
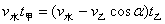 ,② ,②
将①代入②式有  ③ ③
由于 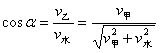 ④ ④
将④式两边平方并整理可得:  ⑤ ⑤
进一步整理得  ⑥ ⑥
比较③、⑥两式可得 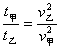
解法二:由已知条件和图中的几何关系可得 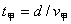 ①, ①, 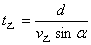 ② ②
利用 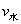 相同得 相同得 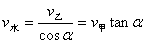 ,建立以上三式可解得 ,建立以上三式可解得 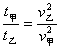
[例2] 如图所示,两根长度均为 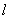 的细线,将质量为m的小球系在竖直转轴上,当两细线拉直时,与竖直方向的夹角均为 的细线,将质量为m的小球系在竖直转轴上,当两细线拉直时,与竖直方向的夹角均为  ,求在下列条件下,两线受到的拉力 ,求在下列条件下,两线受到的拉力
(1)转轴转动角速度为 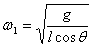 。 。
(2)转轴转动角速度为  。 。

分析与解:当两细线拉直时,两线与竖直方向的夹角均为  ,上段线一定受拉力的作用,而下段线由于旋转角速度不同,可能受到拉力的作用,也可能恰好不受力。因此,我们可先判定下段线刚拉直而恰好不受力的临界角速度 ,上段线一定受拉力的作用,而下段线由于旋转角速度不同,可能受到拉力的作用,也可能恰好不受力。因此,我们可先判定下段线刚拉直而恰好不受力的临界角速度 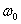 。 。
由受力分析知,小球受上段线拉力 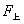 和重力 和重力 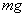 的作用,其合力提供小球做匀速圆周运动的向心力,即: 的作用,其合力提供小球做匀速圆周运动的向心力,即:
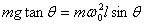 ,得 ,得  。 。
(1)当 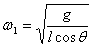 时,恰好等于临界角速度 时,恰好等于临界角速度 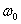 ,所以 ,所以  ; ;
(2)当  时, 时,  两线均拉紧,即对小球都有拉力,由受力分析知: 两线均拉紧,即对小球都有拉力,由受力分析知:
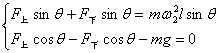
联立解得: 
由此题可以看出:
(1)临界值是圆周运动中一个经常考查的重点内容,它是物体在做周圆运动过程中,发生质变的数值或使物体受力情况发生变化的要害数值。如本题再追加一问即  ,若小球仍能在水平面上做匀速运动,则下段细线将松驰,上段细线与竖直转轴的夹角小于 ,若小球仍能在水平面上做匀速运动,则下段细线将松驰,上段细线与竖直转轴的夹角小于  。 。
(2)长为 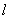 的轻杆一端连一个小球,在竖直平面内做圆周运动与长为 的轻杆一端连一个小球,在竖直平面内做圆周运动与长为 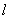 的细线拴一小球,以竖直平面内做圆周运动。在最高点其线速度的最小值,即临界值是不相同的。同学们通过对类似问题的比较,要达到触类旁通、举一反三的效果,那我们就一定能学好物理。 的细线拴一小球,以竖直平面内做圆周运动。在最高点其线速度的最小值,即临界值是不相同的。同学们通过对类似问题的比较,要达到触类旁通、举一反三的效果,那我们就一定能学好物理。
【模拟试题】
1. 关于曲线运动,下列说法正确的是( )
A. 曲线运动一定是变速运动
B. 变速运动不一定是曲线运动
C. 曲线运动可能是匀变速运动
D. 曲线运动其加速度方向一定改变
2. 下列关于圆周运动的说法中正确的是( )
A. 作匀速圆周运动的物体,所受合外力一定指向圆心
B. 作圆周运动的物体,其加速度可以不指向圆心
C. 作圆周运动的物体,其加速度一定指向圆心
D. 作匀速圆周运动的物体,其加速度是不变的
3. 物体受到几个外力的作用而做匀速直线运动,假如撤掉与速度共线的一个力,其它力不变,则它有可能( )
A. 做匀速直线运动 B. 做匀加速直线运动
C. 做匀减速直线运动 D. 做曲线运动
4. 如图所示,两轮用皮带传动,没有打滑,A、B、C三点位置见图示, 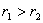 ,O1C= ,O1C=  ,则这三点的向心加速度的关系为( ) ,则这三点的向心加速度的关系为( )
A.  B. B. 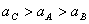
C.  D. D. 
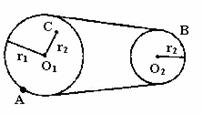
5. 如图所示,物体在恒力F作用下沿曲线从A运动到B,这时,忽然使它所受力反向,大小不变,即由  变为 变为 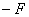 。在此力作用下,物体以后的运动情况,下列说法中不正确的是( ) 。在此力作用下,物体以后的运动情况,下列说法中不正确的是( )
A. 物体不可能沿曲线Ba运动 B. 物体不可能沿直线Bb运动
C. 物体不可能沿曲线Bc运动 D. 物体不可能沿曲线B返回A

6. 如图所示,把一个长为20cm,劲度系数为360N/m的弹簧,一端固定,作为圆心,弹簧的另一端连接一个质量为0.50kg的小球,当小球以 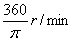 的转速在光滑水平面上做匀速圆周运动时,弹簧的伸长应为( ) 的转速在光滑水平面上做匀速圆周运动时,弹簧的伸长应为( )
A. 5.2cm B. 5.3cm C. 5.0cm D. 5.4cm
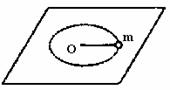
7. 如图所示,一个内部光滑的圆锥桶的轴线垂直于水平面,圆锥桶固定不动。有两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面作匀速圆周运动,则( )
A. 球A的线速度必定小于球B的线速度
B. 球A的角速度必定小于球B的角速度
C. 球A的运动周期必小于球B的运动周期
D. 球A对筒壁的压力必定大于球B对筒壁的压力
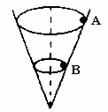
8. 长度为L=0.50m的轻质杆OA,A端有一质量为m=3kg的小球,如图所示,小球以O点为圆心在竖直平面内作圆周运动,通过最高点时小球的速率为2m/s(g取10m/s2),则此时细杆OA受到( )
A. 6N的拉力 B. 6N的压力
C. 24N的拉力 D. 24N的压力

9. 某人站在电动扶梯上不动,经时间t1,由一楼升到二楼,假如电动扶梯不动,人从一楼走到二楼的时间为t2,现在扶梯正常运行,人也保持原来的速率沿扶梯向上走,则人从一楼走到二楼的时间为__________。
10. 物体从高处被水平抛出后,第3.0s末速度方向与水平方向成45º角,那么,物体的初速度为_________,第4.0s末的速度大小为__________。(设4.0s末物体还在空中运动,g=10m/s2)
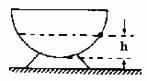
11. 如图所示,半径为R的半球形碗内表面光滑,一质量为m的小球以角速度ω在碗内一水平面做匀速圆周运动,则该平面离碗底的距离h=_________。
12. 某人驾驶摩托车,行至某处碰到5m宽的沟,若对面比此处低4.9m,则此人骑车的速度超过__________时就可跃过。
13. 做匀速圆周运动的物体,线速度为l0m/s,物体从A到B的速度增量大小为l0m/s,已知A、B间弧长是3.14m,则A、B弧长所对的圆心角为_________。圆的半径为__________,向心加速度的大小为__________。
14. 如图所示,实线为某质点作平抛运动轨迹的一部分,测得AB,BC间的水平距离为 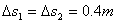 ,高度差 ,高度差  , ,  ,由此可知质点平抛的初速度v0=_________m/s,抛出点到A点的水平距离为__________m,竖直距离为__________m ,由此可知质点平抛的初速度v0=_________m/s,抛出点到A点的水平距离为__________m,竖直距离为__________m

15. 在490m的高空,以240m/s的速度水平飞行的轰炸机,追击一鱼雷艇,该艇正以25m/s的速度与飞机同方向行驶,问:飞机应在鱼雷艇后面多远处投下炸弹,才能击中该艇?
16. 如图,长为R的轻杆一端固定着质量为m的小球,以另一端为轴在竖直面内匀速转动,求下列两种情况下小球转动的角速度ω的值:
(1)当球转至最高点时,若小球对棒作用力为0;
(2)当球转至最高点时,若小球对棒作用力为 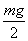
17. 如图,汽车质量为 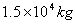 ,以不变的速率先后驶过凹形路面和凸形路面,路面圆弧半径均为15m,假如路面承受的最大压力不得超过 ,以不变的速率先后驶过凹形路面和凸形路面,路面圆弧半径均为15m,假如路面承受的最大压力不得超过  ,汽车答应的最大速率是多少?汽车以此速率驶过路面的最小压力是多少?(g取10m/s2) ,汽车答应的最大速率是多少?汽车以此速率驶过路面的最小压力是多少?(g取10m/s2)

18. 在光滑水平面内建立xoy坐标系,质量为m=4kg的质点正沿y轴正方向匀速运动,其速度为v0=2m/s。如图所示,当质点运动到原点O处时开始受到沿 x方向的恒力F作用。
(1)若要使质点能经过坐标为(4,2)的p点,则恒力F大小为多大?
(2)设质点自O点经过一段时间后到达某点q,其坐标为(x0,y0),若作质点运动轨迹在q点的切线,则切线反向延长线与y轴相交,交点纵坐标一定为y0/2,试证实。
【试题答案】
1. ABC 2. AB 3. BC 4. C 5. C 6. C 7. B 8. B
9.  10. 10. 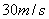 , , 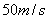
11.  12. 12. 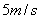 13. 13.  , ,  , , 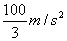
14. 4,0.8,0.2
15. 由 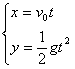 得: 得: 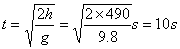
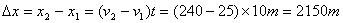
故飞机应在鱼雷艇后面2150m远处投下炸弹,才能击中该艇。
16.
① 由  得: 得: 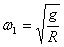 ②若N为支持力, ②若N为支持力,
则:   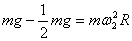 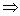 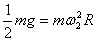 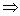 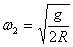 ; ;
若N为压力,则
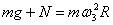 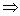 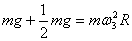 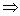 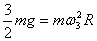 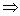 
17. 由  得: 得: 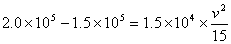 ,所以: ,所以:
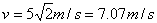 。由 。由 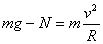 得: 得: 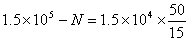 , ,
所以: 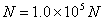
18.
(1)由 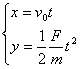 得 得 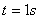 , , 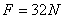 。(2)略 。(2)略
|