机械能守恒定律·典型题剖析

例1　 关于机械能是否守恒的叙述，正确的是　　　 [　　　 ]

A．作匀速直线运动的物体的机械能一定守恒．

B．作匀变速运动的物体机械能可能守恒．

C．外力对物体做功为零时，机械能一定守恒．

D．只有重力对物体做功，物体机械能一定守恒．

分析　 机械能守恒的条件是除重力或弹性力对物体做功外，没有其他外力对物体做功，或其他外力对物体做功的代数和等于零．D正确．

当物体作匀速直线运动时，除重力对物体做功外，可能还有其他外力做功．如降落伞在空中匀速下降时，既有重力做功，又有阻力做功，机械能不守恒．A错．

物体作匀变速运动时，可能只有重力对物体做功，如自由落体运动，此时物体的机械能守恒．B正确．

因物体所受的外力，指的是包括重力在内的所有外力，当外力对物体做功为零时，可能是处于有介质阻力的状态，如匀速下降的降落伞，所以机械能不一定守恒．C错．

答　 B，D．

例2　 a、b、c三球自同一高度以相同速率抛出，a球竖直上抛，b球水平抛出，c球竖直下抛．设三球落地的速率分别为va、vb、vc，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 [　　　 ]

A．va＞vb＞vc．

B．va=vb＞vc．

C．va＞vb=vc．

D．va=vb=vc．

分析　 小球抛出后，只有重力对它做功，所以小球从抛出到落地过程中的机械能守恒．

设抛出的速率为v0，抛出处高度为h，取地面为零势能位置，由

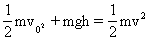
得落地速率

可见，它仅与抛出时的速率及离地面的高度有关，与抛出的方向无关．

答　 D．

说明　 由本题解答可知，从一定高度h以一定大小的初速度v0抛出的物体，落地时的速度大小恒为

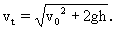
它与抛出时的方式——竖直上抛、下抛、平抛、斜上抛、斜下抛等无关，不同的抛出方式只影响着物体在空中的具体路径、运动时间以及落地速度的方向．

例3　 用一根长l的细线，一端固定在顶板上，另一端拴一个质量为m的小球．现使细线偏离竖直方向α角后，从A处无初速地释放小球（图4-21）．试问：

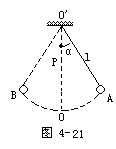
（1）小球摆到最低点O时的速度？

（2）小球摆到左方最高点的高度（相对最低点）？

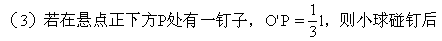
向左摆动过程中能达到的最大高度有何变化？

分析　 小球在摆动过程中，受到两个力作用：重力和线的拉力．由于小球在拉力方向上没有位移，拉力对小球不做功，只有重力做功，所以小球在运动过程中机械能守恒．

解答　 （1）设位置A相对最低点O的高度为h，取过O点的水平面为零势能位置．由机械能守恒得

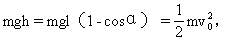
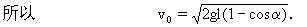
（2）由于摆到左方最高点B时的速度为零，小球在B点时只有势能．由机械能守恒

EA=EB

即　　　　　　　　　　　　　　　　　　　　　　　 mgh=mgh'．

所以B点相对最低点的高度为

h'=h．

（3）当钉有钉子P时，悬线摆至竖直位置碰钉后，将以P为中心继续左摆．由机械能守恒可知，小球摆至左方最高点B1时仍与AB等高，如图4-22所示．

说明　 第（3）小题中的钉子在竖直线上不同位置时，对小球的运动是有影响的．当钉子位于水平线AB上方时，小球碰钉后总能摆到跟AB同一高度处．若钉子继续下移，碰钉后的运动较为复杂，有爱好的读者可自行研究．

讨论

1．机械能守恒定律的研究对象

机械能的转化和守恒是指系统而言．动能与重力势能的转化是指物体与地球组成的系统机械能守恒；动能与弹性势能的转化是指物体与弹簧组成的系统机械能守恒．通常说某物体的机械能守恒是一种简化的不严格的说法．前面介绍的动能公式，则是对单个物体（质点）而言的．

2．机械能守恒定律的应用特点

应用机械能守恒定律时，只需着重于始末两状态的分析，不需考虑中间过程的细节变化，这是守恒定律的一大特点．如例2中没有从具体的抛出方式的不同规律出发，但根据机械能守恒却很轻易求解．