牛顿第二定律典型题剖析

牛顿第二定律·典型题剖析

例1　 在光滑水平面上的木块受到一个方向不变，大小从某一数值逐渐变小的外力作用时，木块将作　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 [　　　 ]

A．匀减速运动．　　　　　 B．匀加速运动．

C．速度逐渐减小的变加速运动．

D．速度逐渐增大的变加速运动．

分析　 木块受到外力作用必有加速度．已知外力方向不变，数值变小，根据牛顿第二定律可知，木块加速度的方向不变，大小在逐渐变小，也就是木块每秒增加的速度在减少．由于加速度方向与速度方向一致，木块的速度大小仍在不断增加，即木块作的是加速度逐渐减小、速度逐渐增大的变加速运动．

答　 D．

说明　 物体的加速度只与它受到的外力有联系，当外力逐渐减小到零时，物体的速度恰增大到最大值vm．以后，物体就保持这个速度沿光滑水平面作匀速直线运动，这个物体的v－t图大致如图3－5所示．

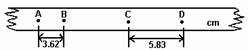
例2　 如图3－6所示，底板光滑的小车上用两个量程为20N、完全相同的弹簧秤甲和乙系住一个质量1kg的物块．在水平地面上当小车作匀速直线运动时，两弹簧秤的示数均为10N．当小车作匀加速直线运动时，弹簧秤甲的示数变为8N．这时小车运动的加速度大小是　　　　　　　　　　　　　　　　　 [　　　 ]

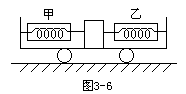
A．2m/s2．　　　　　　　　　　 B．4m/s2．

C．6m/s2．　　　　　　　　　　 D．8m/s2．

分析　 因弹簧的弹力与其形变量成正比，当弹簧秤甲的示数由10N变为8N时，其形变量减少，则弹簧秤乙的形变量必增大，且甲、乙两弹簧秤形变量变化的大小相等，所以，弹簧秤乙的示数应为12N．物体在水平方向所受到的合外力为

F=T乙-T甲=12N-8N=4N．

根据牛顿第二定律，得物块的加速度大小为

答　 B．

说明　 无论题中的弹簧秤原来处于拉伸状态或压缩状态，其结果相同．读者可自行通过对两种情况的假设加以验证．

例3　 汽车空载时的质量是4×103kg，它能运载的最大质量是3×103kg．要使汽车在空载时加速前进需要牵引力是2.5×104N，那么满载时以同样加速度前进，需要的牵引力是多少？

分析　 由空载时车的质量和牵引力算出加速度，然后根据加速度和满载时的总质量，再由牛顿第二定律算出牵引力．

解答　 空载时，m1=4×103kg，F1=2.5×104N，由牛顿第二定律得加速度：

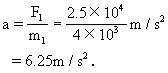
满载时，总质量为m1 m2＝7×103kg，同理由牛顿第二定律得牵引力：

F2=（m1 m2）a=7×103×6.25N

=4.375×104N．

说明　 根据牛顿第二定律F=ma可知，当加速度a相同时，物体所受的合外力与其质量成正比．因此可以不必先算出加速度的大小，直接由比例关系求解．即由

直接得

根据牛顿第二定律，当加速度a相同时，各个物体（或各个部分）所受的合外力与其质量成正比．用公式可表示为

F1∶F2∶F3∶…Fn＝m1∶m2∶m3∶…mn，

或Fi∶F合=mi∶∑m．

式中Fi表示质量为mi的物体所受的合外力，F合表示总质量为∑m=m1 m2 … mn的整个物体系统所受的合外力．

利用合外力与质量的这种比例关系，解题中常会带来很大的方便（如例3）