|
4、明确研究对象,引出课题
这节课我们就重点来研究这样的数。(板书课题:正负数)
让我们再来读几个正负数。(课件:+100、-75、-1.8、38)这个38前面怎么没有符号?你认为它是正数还是负数?为了简便正数前可以不写正号。谁能来说几个正负数?(生:……)说得完吗?说不完怎么办?(板书:……)谁再来说几个负数?(生:……)说得完吗?(板书:……)正数前的正号可以省略不写,那么负数前的负号可以去掉吗?为什么?
5、出示史料,进一步了解负数的历史。
师:看来啊,负数的出现还真得是很有必要,那你知道哪个国家最早出现了负数吗?猜一猜?(生:……)让我们通过一段资料一起来回顾负数的历史。
(边放课件边介绍)“中国是世界上最早认识和应用负数的国家。早在两千多年前的《九章算术》中,就有正数和负数的记载。在古代人民生活中,以收入钱为正,以支出钱为负。在粮食生产中,以产量增加为正,以产量减少为负。古代的人们为区别正、负数,常用红色的算筹表示正,黑色的算筹表示负。而西方国家认识正、负数则要迟于中国数百年。”
请学生谈感受。
三、动手操作,建立概念
(一)通过拨温度计了解比较正负数大小的方法。
(课件:没有标刻度的温度计)师:昨天我们已经知道用温度计可以测量温度,今天咱们就亲自动手来拨温度计。每格代表2℃,谁能拨出6℃?(生:拨不出来)为什么?(没有0℃。要先找到0℃,这是分界点。)(板书:0)(课件出示刻度)再请学生拨20℃。
师:比较这两个温度,你有什么发现?(越往上温度越高;20比6大,所以20℃比6℃温度高。)再拨—6℃和—20℃。比较两个温度(—6℃和—20℃)哪个更冷?为什么?(温度计上越往下温度越低、—20℃在—6℃下面。)负数怎样比大小?(和正数相反。数大的加上负号后反而变小,数小的加上负号后反而变大)谁能用你的动作和表情告诉大家—20℃时的感觉。(生做)我国新疆地区最冷时温度达到-40℃,大概在温度计的哪儿?(生找-40℃的大概位置)
(二) 总结归纳正、负数和0的关系。
师:借助温度计我们对正数和负数有了更深的了解,现在黑板上有很多的数,很乱,我们来给它们分分类好吗?谁能用一个圈把所有的正数圈出来,再用一个圈把所有的负数圈出来。(生圈)(注意:要把省略号也圈进去)0表示什么呢?(生:0是分界点)那0属于正数还是负数呢?(生:0既不是正数,也不是负数)那0和正数与负数之间的大小关系是怎么样的呢?你能用大于号或小于号把它们连接起来吗?(板书:正数 > 0 >负数)这是我们今天得出的很重要的两个结论。(课件:所有的正数都比0大,所有的负数都比0小,0既不是正数,也不是负数)
四、借助实例,解释应用
(一)引导学生举例:请同学们回忆一下,生活中你还曾经在哪见过正负数?(生举例:……)
(二)重点讨论
1、用正负数记录小明家的收支情况。(课件:课本89页“练一练”第1题。)
2、电梯中的正、负数。
(课件:叔叔上五楼开会,阿姨要到地下二楼取车,应该按哪两个键?)
3、海拔高度中的正、负数。
(课件:海平面图)黄山的最高峰莲花峰比海平面高出1864米,记作+1864米。吐鲁番盆地比海平面低155米,记作( )米。
4、下图每格表示1米,小华刚开始的位置在0处。(课件:课本89页“练一练”第2题。)
A小华从0点向东行5米,表示为+5,那么从0点向西行3米,表示为( )米。
B如果小华的位置是+7米,说明他是向( )行( )米。
C如果小华的位置是-8米,说明他是向( )行( )米。
5、刘翔在第十届世界田径锦标赛半决赛中,110米栏的成绩是13.42秒,当时赛场风速为每秒-0.4米。
讨论:风速怎么会有负的呢?(请两生分别代表刘翔和风速表演,是相反的)
师:如果风速是+0.4米,又是什么意思呢?(再请学生表演)
五、总结
师:生活中有更多的负数等着同学们去探索、发现,只要同学们细心观察,一定会用我们所学的知识发现问题、解决问题!
附板书设计:
正负数
正数 > 0 >负数
进球 +3 -2 丢球
转入 +25 -18 转走
赚钱 +6000 -2000 亏钱
…… ……
教学反思:
《正负数》一课是北师大版四年级上册第七单元的第二课时,它的上一课是《温度》,在这一节课中学生已经了解了可以在数的前面加+和-来表示零上温度和零下温度,而且也已经知道0℃既不属于零上温度也不属于零下温度。但并没有引入正数和负数的概念。《正负数》一课就是让学生在认识温度的基础上进一步地认识正负数以及0的特殊意义。
课前我也查阅了一些相关的资料,在取其精华的基础上又进行了进一步的改进。主要体现在如下几个方面:
一、课前游戏
上课之前,我利用两三分钟的时间带领学生做了一个简单的游戏:说反义词,既活跃了课堂的气氛,又让学生初步感知了一些具有相反意义的量。
二、通过记录相反意义的量,初步了解负数的意义。
上课伊始,我首先请学生用自己喜欢的方法记录三组相反意义的量,课堂上学生根据已有的经验,呈现出多种不同的记录方法。最后由学生自己总结出正负数的表示方法。紧接着我又强化了正数分别代表了足球比赛中的进球、转学人数中的转入和做生意中的赚钱以及负数代表的丢球、转出和亏钱并板书在黑板上,为下一步学习“0既不是正数也不是负数”埋下伏笔。
三、总结归纳正、负数和0的关系。
“0既不是正数也不是负数”是本节课的难点。通过温度的学习学生已经初步感知0℃既不属于零上温度也不属于零下温度,但当我让学生用一个圈把所有的正数圈起来,再把所有的负数都圈起来时,部分学生仍然认为0是正数。这时我没有急于告诉学生答案,而是先让学生进行争论,当学生争论到我认为时机成熟之际,我引导学生看黑板上的板书,并问:“我们已经知道0℃既不属于零上温度也不属于零下温度,那谁能结合刚才的例子来说说0到底是什么数呢?”马上有学生回答出:“0既不是进球也不是丢球、既不是转来也不是转走、既不是赚钱也不是亏钱,所以0既不是正数也不是负数!”这一番有力的论证让刚才所有认为0是正数的同学口服心服。
四、借助实例,解释应用
为进一步巩固对正负数的认识,让学生充分感受到正负数在生活中的作用,在这个环节中,我让学生充分举了生活中的正负数的例子,学生的思维非常活跃,有一个学生举出了“课堂中答对奖励答错罚能用正数和负数表示”,还有个同学竟然想到“爸爸在电脑上打牌时赢了是正分,输了是负分”的例子。紧接着我又“趁热打铁”,安排了“电梯中的正、负数”、“海拔高度中的正、负数”、“小华的位置”及“跑步时风速为何为负”等一系列的练习,这个环节给学生提供了充分的思维和交流的空间,使学生的思维之翼展翅翱翔。
四年级的学生已经有了一定的生活经验,在设计这节课的时候,我尽可能地从生活中找素材并将所学的知识运用到生活中去,并争取让学生自己发现和感受,做到人人参与学习,人人学有价值的数学。
教学目标
1.使学生理解正数与负数的概念,并会判断一个给定的数是正数还是负数;
2. 会初步应用正负数表示具有相反意义的量;
3.使学生初步了解有理数的意义,并能将给出的有理数进行分类;
4.培养学生逐步树立分类讨论的思想;
5. 通过本节课的教学,渗透对立统一的辩证思想。
教学建议
一、重点、难点分析
本课的重点是了解正数与负数是由实际需要产生的以及有理数包括哪些数。难点是学习负数的必要性及有理数的分类。关键是要能准确地举出具有相反意义的量的典型例子以及要明确有理数分类的标准。
正、负数的引入,有各种不同的方法。教材是由学生熟知的两个实例:温度与海拔高度引入的。比0℃高5摄氏度记作5℃,比0 ℃低5摄氏度,记作-5℃;比海平面高8848米,记作8848米,比海平面低155米记作-155米。由这两个实例很自然地,把大于0的数叫做正数,把加“-”号的数叫做负数;0既不是正数也不是负数,是一个中性数,表示度量的“基准”。这样引入正、负数,不仅有利于学生正确使用正、负数表示具有相反意义的量,而且还将帮助学生理解有理数的大小性质。把负数理解为小于0的数。教材中,没有出现“具有相反意义的量”的概念。这是有意回避或淡化这个概念。目的是,从正、负数引入一开始就能较深刻的揭示正、负数和零的性质,帮助学生正确理解正、负数的概念。
关于有理数的分类要明确的是:分类标准不同,分类结果也不同,分类结果应是不重不漏,即每一个数必须属于某一类,又不能同时属于不同的两类。
二、知识结构
1.正数、负数和零的概念
|
正数 |
负数 |
零 |
|

象1、2.5、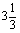 、48等大于零的数叫正数 、48等大于零的数叫正数 |
象-1、-2.5,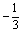 ,-48等小于零的数叫负数 ,-48等小于零的数叫负数 |
0叫做零,0既不是正数也不是负数 |
2.有理数的分类


三、教法建议
这节课是在小学里学过的数的基础上,从表示具有相反意义的量引进负数的.从内容上讲,负数比非负数要抽象、难理解.因此在教学方法和教学语言的选择上,尽可能注意中小学的衔接,既不违反科学性,又符合可接受性原则。例如,在讲解有理数的概念时,让学生清楚地认识有理数与算术数的根本区别,有理数是由两部分组成:符号部分和数字部分(即算术数).这样,在理解算术数和负数的基础上,对有理数的概念的理解就简便多了.
为了使学生掌握必要的数学思想和方法,在明确有理数的分类时,可以有意识地渗透分类讨论的思想方法,理解分类的标准、分类的结果,以及它们的相互联系。通过正数、负数都统一于有理数,可以将对立统一的辩证思想的逐步树立渗透到日常教学中。
上一页 [1] [2] [3] [4] 下一页
|