中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料
|
|
| 中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
二、本题共4小题；每小题5分，共20分.把答案填在题中的横线上. 11.容积为100 L的贮气钢瓶中，贮有压强为4.0×106 Pa，温度为17℃的氧气，试估算钢瓶内氧分子的个数为 个.（标准大气压强p0=1.0×105 Pa,阿伏加德罗常数N=6.0×1023 mol-1,要求保留一位有效数字） 12.一根长为l的直导线，在垂直于匀强磁场的平面内，绕轴O以角速度ω逆时针匀速转动，如图3—9所示，以O为圆心，l/2为半径的圆形区域内磁场方向垂直纸面向里，这个圆形区域以外的磁场方向垂直纸面向外，两个磁场的磁感应强度大小均为B，导线在旋转过程中aO间的电势差UaO= .
图3—9 13.已知基态氢原子能量为E1，普朗克恒量为h，氢原子从n=3的能级跃迁到n=2的能级时，辐射的光照到某金属恰能发生光电效应，该金属的极限频率ν0= ；一群处于n=4能级的氢原子自发地向低能级跃迁，辐射的光照射到该金属时产生光电效应，这束光中能使金属发生光电效应的光谱线共有 条. 14.某一星球的第一宇宙速度为v，质量为m的宇航员在这个星球表面受到的重力为W，由此可知这个星球的半径是 . 三、本题共3小题；其中第15题4分,第16题8分，第17题10分，共22分.把答案填在题中的横线上或按题目要求作图. 15.在一些用来测一角度的仪器上，有一个可转动的圆盘，圆盘的边缘标有角度刻度.为了较准确地测量出圆盘转动的角度，在圆盘外侧有一个固定不动的游标，上面共有10个分度，游标总角度为9度.图3—10画出游标和圆盘的一部分.读出此时圆盘的零刻度线相对于游标零刻度线转过的角度为 度.
图3—10 16.为了测定一个“6 V，1 W”的灯泡在不同电压下的电功率，现有器材如下：
| 直流电源
| 电动势6 V
| 内阻不计
| 直流电流表A1
| 量程200 mA
| 内阻约2 Ω
| 直流电流表A2
| 0~0.6 A
| 内阻约0.5 Ω
| 直流电压表V1
| 0~3 V
| 内阻约5×103 Ω
| 直流电压表V2
| 0~15 V
| 内阻约1.5×104 Ω
| 滑线变阻器
| 电阻值0~15 Ω
| 额定电流1 A
| 开关一个
|
|
| 导线若干根
|
| |
测量时要求电灯两端电压从0 V开始连续调节，尽量减小误差，测多组数据.应选择电流表（用序号表示），电压表；在图3—11所示的虚线框内画出测量的电路图.
图3—11 图3—12
17.实验室有下列器材：
A.电流表（ 0~ 100 μA ,100 Ω）
B.电流表（0~ 1 mA，1 kΩ）
C.变阻器（0~300 Ω）
D.变阻器（0~800 Ω）
E.干电池（1.5 V，内阻不计）
F.干电池（9 V，内阻不计）
现要安装一只欧姆表，从上述备用器材中，电流表应选用 ，变阻器应选用 ，电源应选用 .
在图3—12方框中画出欧姆表的电路图并标出红黑表笔.
四、本题共5小题，68分.解答应写出必要的文字说明、方程式和重要演算步骤.只写出最后答案的不能得分.有数值计算的题，答案中必须明确写出数值和单位.
18.(12分)设人造地球卫星绕地球做匀速圆周运动.根据万有引力定律、牛顿运动定律及周期的概念，论述人造地球卫星随着轨道半径的增加，它的线速度变小，周期变大.
19.（12分）某种液体的折射率为 
，在其液面下有一可绕O轴匀速转动的平面镜OA，OA的初始位置与液面平行，如图3—13所示.在液面与平面镜间布满自左向右的平行光线.若在平面镜逆时针旋转一周的过程中，光线射入空气中的时间为2 s.试问：（1）平面镜由初始位置转过多大角度时，光线开始进入空气？
（2）平面镜旋转的角速度多大？
20.(14分)如图3—14所示，光滑水平面右端B处连接一个竖直的半径为R的光滑半圆轨道，在离B距离为x的A点，用水平恒力将质量为m的质点从静止开始推到B处后撤去恒力，质点沿半圆轨道运动到C处后又正好落回A点，求：
图3—14
(1)推力对小球所做的功.
(2)x取何值时，完成上述运动所做的功最少?最小功为多少？
(3)x取何值时，完成上述运动用力最小?最小力为多少？
21.（14分）如图3—15所示，在真空区域内，有宽度为L的匀强磁场，磁感应强度为B，磁场方向垂直纸面向里，MN、PQ是磁场的边界，质量为m，带电为－q的粒子，先后两次沿着与MN夹角为θ(0＜θ＜９０°)的方向垂直磁感线射入匀强磁场B中.第一次，粒子是经电压U1加速后射入磁场，粒子刚好没能从PQ边界射出磁场；第二次粒子是经电压U2加速后射入磁场，粒子刚好垂直PQ射出磁场.（不计重力影响）求：
图3—15
(1)为使粒子经电压U2加速射入磁场后沿直线射出PQ边界，可在磁场区域加一匀强电场，求该电场的场强大小和方向.
(2)加速电压 
的值.
22. (16分)为了证实玻尔关于原子存在分立能态的假设，历史上曾经有过闻名的夫兰克—赫兹实验，其实验装置的原理示意图如图3—16所示.由电子枪A射出的电子，射进一个容器B中，其中有氦气.电子在O点与氦原子发生碰撞后，进入速度选择器C，然后进入检测装置D.速度选择器C由两个同心的圆弧形电极P1和P2组成，当两极间加以电压U时，只答应具有确定能量的电子通过，并进入检测装置D.由检测装置测出电子产生的电流I，改变电压U，同时测出I的数值，即可确定碰撞后进入速度选择器的电子的能量分布.
我们合理简化问题，设电子与原子碰撞前原子是静止的，原子质量比电子质量大很多，碰撞后，原子虽然稍微被碰动，但忽略这一能量损失，设原子未动（即忽略电子与原子碰撞过程中，原子得到的机械能）.实验表明，在一定条件下，有些电子与原子碰撞后没有动能损失,电子只改变运动方向.有些电子与原子碰撞时要损失动能，所损失的动能被原子吸收，使原子自身体系能量增大，
(1)设速度选择器两极间的电压为U（V）时，答应通过的电子的动能为Ek（eV），导出Ek（eV）与U（V）的函数关系（设通过选择器的电子的轨道半径r=20.0 cm，电极P1和P2之间隔d=1.00 cm,两极间场强大小处处相同），要说明为什么有些电子不能进入到接收器.
(2)当电子枪射出的电子动能Ek=50.0 eV时，改变电压U（V），测出电流I（A），得出下图所示的I—U图线，图线表明，当电压U为5.00 V、2.88 V、2.72 V、2.64 V时，电流出现峰值，定性分析论述I—U图线的物理意义.
(3)根据上述实验结果求出氦原子三个激发态的能级En（eV），设其基态E1=0.
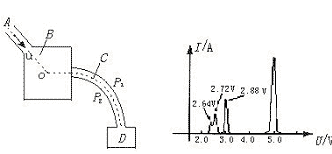
图3—16
| |
3.考试结束，将本试卷和答题卡一并交回．
