小船渡河问题

例1 一条宽度为L的河，水流速度为为v水，已知船在静水中的航速v船，那么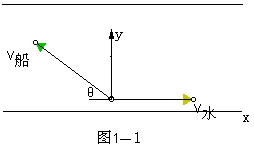

（1）怎样渡河时间最短？

（2）若v水＜v船，怎样渡河位移最小？

（3）若v水＞v船，怎样渡河船漂下的距离最短？

【分析与解答】：

(1)如图1—1所示，设船的航向与河岸成任意角θ斜向上，这时船速在y轴方向上的分速度为v y=v船sinθ,渡河所需的时间为L/v船sinθ

可以看出：在L、v船一定时，t随sinθ增大而减小；当θ=900时，sinθ=1,最大，即船头与河岸垂直时，渡河时间最短，且tmin=L/v船

(2)如图1—2所示，渡河的最小位移即河的宽度L,要使渡河位移等于L,必须使船的合速度v的方向与河岸垂直。此时船沿河岸方向的速度分量vx=0，这时船头应指向河的上游，并与河岸成一定的角度θ， 即v水-v船cosθ=0，θ=arccosv水/v船

因为0≤θ≤1，所以只有在v水＜v船时，船才有可能垂直河岸横渡。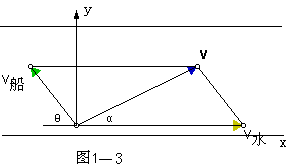

(3)则不论船的航向如何，总要被水冲向下游，怎样才能使船的航程最短呢？如图1—3所示，设船头(v船)与河岸成θ角，合速度(v)与河岸成α角，可以看出：α角越大，船到下游的距离x越短。那么，在什么条件下，α角最大呢？请看 课件(请安装几何画板)

可见，以v水的矢尖为圆心，为半 径画圆，当与圆相切时如图1—4，角最大。 此时sinα=v船/v水，

船的最短航程为s=d/sinα=dv船/v水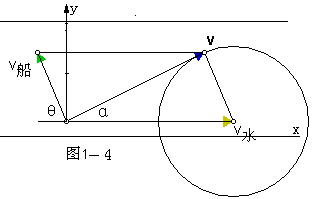

渡河问题参考课件（flash）

可见，正交分解是解决渡船问题的一种比较好的方法

绳子拉船问题

一个速度岸矢量运算法则分解为两个分速度，可以有无数组解，但若与实际情况不服，则所得分速度就毫无物理意义。所以速度分解的一个基本原则就是按实际效果来进行分解。常用的思想方法有两种：

一种思想是现虚拟合运动的一个位移，看看这个位移产生了什么效果，从中找到运动分解的办法；

另一种思想方法实现确定合运动的速度方向（这里有一个简单的原则：物体的实际运动方向就是合速度的方向），然后分析有这个合速度所产生的实际效果，以确定两个分速度的方向。

例2：如图2-1所示，用绳牵引小船靠岸，若收绳的速度为v1，在绳子与水平方向夹角为α的时刻，船的速度v有多大？

【分析与解答】：方法一：虚拟小船在Δt时间内从A移过Δs到达C如图2—2所示，这个运动可设想为两个分运动所合成：先被绳拉过Δs1到B，再随绳绕滑轮O点做圆周运动到C点，位移为Δs2

因为OB=OC，∠OBC=β=(180-Δθ)/2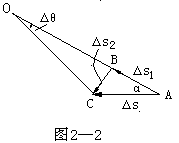

若Δt很小很小，Δθ→0，则β→900，即Δs2与Δs1垂直，此时有Δs1=Δscosα,也 就是Δs1/Δt=（Δs/Δt）cosα，则v1=vcosα，v=v1/cosα。

方法二：船的速度v的方向就是合运动的速度方向。由于这个v产生两个效果：一是使绳系着小船的一端沿绳拉方向以速率v1运动；二是师生的这段绕滑轮做顺时针方向的圆周运动，那么合 速度v应沿着绳子的牵引方向和垂直于绳子的方向分解如图2—3所示，从图中可知：v=v1/cosα.