|
万有引力综合应用(2)·典型例题解析
【例1】关于人造地球卫星,下列说法正确的是(已知地球半径为6400km)
[ ]
A.运行的轨道半径越大,线速度也越大;
B.运行的速率可能等于8km/s;
C.运行的轨道半径越大,周期也越大;
D.运行的周期可能等于80min.
解析:C正确.
设地球质量为M,卫星质量为m,卫星在轨道半径为r的轨道上运

卫星的运行速率最大,卫星的最大运行速率为7.9km/s.应该指出7.9km/s是卫星在绕地球做圆周运动时的最大速度,当卫星绕地球做椭圆运动时
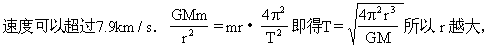
T越大.由周期公式代入g的关系得T的最小值为85min,80min<85min,故D也错.
点拨:本题从几个侧面考查了卫星的问题.从卫星发射,到卫星的运转,以及卫星的宇宙速度.既然是卫星问题总离不开万有引力提供向心力问题,当然是把卫星的运动当成圆周运动看待.
【例2】假如在离月球表面高度为300km处发射月球卫星,它速度应多大?(月球质量m月=7.38×1022kg,月球半径R月=1.67×106m)

【例3】假如地球自转速度加快,地球上物体的重量将发生怎样的变化?地球自转角速度等于多少时,在赤道上物体的重量为零?这时一昼夜将有多长(R地=6370km,M地=5.98×1024kg)
点拨:物体随地球自转所需的向心力是地球对物体引力一部分,在赤道上引力方向与向心力一致.由F心=mω2R可知,当角速度增大时,向心力增大,物体的重力将减小.由F引=F心+G知,当F引=F心
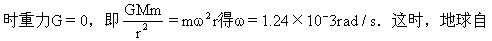
转周期,即一昼夜的时间为T=5067s.
【例4】如图47-1所示,A、B两颗行星绕同一恒星做匀速圆周运动.运动方向相同,A的周期为T1,B的周期为T2,某时刻两行星的距离最近,求:

(1)再经过多长时间两行星的距离又最近?
(2)再经过多长时间,两行星的距离最远?
点拨:两行星转过的角度差为2π的整数倍时,其相距最近,这时三颗星在同一直线上,而且A在中间.两行星转过的角度差为π的奇数倍时,其相距最远,这时三颗星在同一直线上,而且恒星在中间.


(n=1、2、3、…)
跟踪反馈
1.人造地球卫星绕地球做匀速圆周运动,其速率:
[ ]
A.一定等于7.9km/s
B.等于或小于7.9km/s
C.一定大于7.9km/s
D.介于7.9~11.2km/s
2.人造地球卫星运行中由于受大气阻力,轨道半径逐渐减小,则线速度和周期变化情况是
[ ]
A.速度减小,周期增大
B.速度减小,周期减小
C.速度增大,周期增大
D.速度增大,周期减小
3.设想人类开发月球,不断地把月球上的矿藏搬运到地球上.假如经过长时间开采后,地球仍可看成均匀球体,月球仍沿开采前的圆轨道运动,则与开采前比较
[ ]
A.地球与月球间的万有引力将变大
B.地球与月球间的万有引力将变小
C.月球绕地球运动的周期将变长
D.月球绕地球运动的周期将变短
4.天文观测某行星的线速度为v,离太阳距离为r,则可知太阳的质量为_______.已知地球绕太阳公转的线速度约30km/s,轨道半径为1.5×108km,可知太阳的质量为_______kg.(取一位有效数字)
参考答案
1.B 2.D 3.BD 4.rv2/G;2×1030
|