|
圆周运动(二)
知识要点:
深刻理解向心力的概念,知道假如一个力或几个力的合力的效果是使物体产生向心加速度,这一个力或几个力的合力就是向心力,会对圆周运动的物体进行受力分析,会找向心力。知道物体做匀速圆周运动的条件,知道什么是近心运动,什么是离心运动,知道外力大于向心力做近心运动,外力小于向心力,做离心运动。
三. 重难点分析:
1. 向心力及来源
物体做圆周运动有加速度 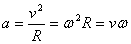 产生这个加速度的力就叫向心力,这个力的大小为 产生这个加速度的力就叫向心力,这个力的大小为  。方向总是指向圆心。只要物体所受外力大小为 。方向总是指向圆心。只要物体所受外力大小为  ,方向总指向圆心,那么这个力就可以做向心力,若几个力的合力大小为 ,方向总指向圆心,那么这个力就可以做向心力,若几个力的合力大小为  ,方向指向圆心,那么这几个力的合力做向心力。因此① 向心力是根据力的效果命名的,不是单独一种性质的力。② 向心力可以由一个力提供也可以由几个力的合力充当,既几个力共同做向心力,还可以由某一个力的分力作向心力。 ,方向指向圆心,那么这几个力的合力做向心力。因此① 向心力是根据力的效果命名的,不是单独一种性质的力。② 向心力可以由一个力提供也可以由几个力的合力充当,既几个力共同做向心力,还可以由某一个力的分力作向心力。
2. 做匀速圆周运动的条件,近心运动,离心运动。当物体做匀速圆周运动,外力或几个外力的合大小 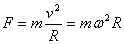 方向总指向圆心,就是做匀速圆周运动所需要的力恰好与合外力相等。 方向总指向圆心,就是做匀速圆周运动所需要的力恰好与合外力相等。
若合外力 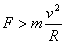 则F所产生的加速度大于 则F所产生的加速度大于 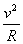 ,在垂直于v方向改变得过快,速度偏向圆心过多,运动半径减小做近心运动。 ,在垂直于v方向改变得过快,速度偏向圆心过多,运动半径减小做近心运动。
若合外力 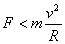 则F所产生的加速度比做半径不变的圆周运动加速度 则F所产生的加速度比做半径不变的圆周运动加速度 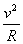 小,偏向圆心方向速度的改变慢,运动的半径增大,做远离圆心的运动简称离心运动。 小,偏向圆心方向速度的改变慢,运动的半径增大,做远离圆心的运动简称离心运动。
3. 实例分析
(1)火车转弯
火车左右两侧的车轮分别沿铁轨运动,沿直线运动时,两条钢轨位于同一水平面内以防侧倾倒。而当火车转弯时,有向心加速度需要向心力,为此使钢轨不在一个平面内,外侧高而内侧低,本身不再是竖直的但能顺利转弯而不发生侧倾,否则车辆不能受到外力,要做离心运动,发生倾覆。
见下图,列车转弯时,靠近圆心一侧为内侧,另一侧为外侧,相应为内轨外轨,与列车前进方向无关。
取水平面内转弯半径为r,内外轨距为d,内外轨高度差为h。
转弯时竖直截面见右图,由于转弯在水平面内转弯半径为水平方向,向心加速度为水平方向。列车受力有重力,竖直向下,路轨支持力  方向与双轨连线垂直,这两个力的合力做向心力,沿水平方为 方向与双轨连线垂直,这两个力的合力做向心力,沿水平方为 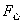 。 。
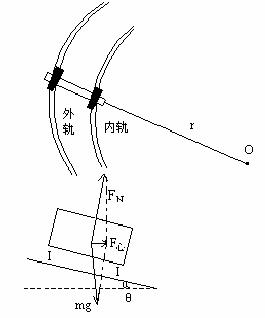
两轨道连线倾角为  , , 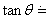 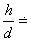 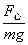
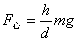 而 而 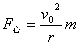  为转弯时速率 为转弯时速率
∴ 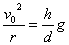 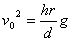 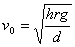
转弯时速率  则外力的合力恰好等于向心力,若 则外力的合力恰好等于向心力,若 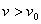 则外力的合力小于向心力,要做离心运动火车向外侧翻倒,滑动,火车对外侧轨道有沿转弯半径向外的压力,火车向外侧推轨道。 则外力的合力小于向心力,要做离心运动火车向外侧翻倒,滑动,火车对外侧轨道有沿转弯半径向外的压力,火车向外侧推轨道。
当  则合外力大于向心力,要做近心运动,火车对内侧轨道有沿转弯半径向圆心方向的压力,即火车对内轨有向圆心方向的推力。 则合外力大于向心力,要做近心运动,火车对内侧轨道有沿转弯半径向圆心方向的压力,即火车对内轨有向圆心方向的推力。
火车提速转弯半径r不改变则内外轨道高差h要增加,不然火车转弯有危险。
(2)汽车过拱形桥和凹形山坡底,设拱形桥半径为r,汽车速率为v。

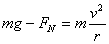 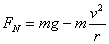 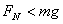 汽车对桥面压力与 汽车对桥面压力与  等大比重力小。 等大比重力小。
若v足够大使  则 则 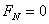 汽车对桥面无压力,汽车即将离开桥面。 汽车对桥面无压力,汽车即将离开桥面。
若汽车没有离开桥面半径与竖直方向成  角, 角, 
即使v不变,  也会随 也会随  增大而减小。当 增大而减小。当 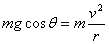 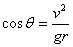
 时, 时,  减小到零,汽车也即将离桥面。 减小到零,汽车也即将离桥面。
(3)圆锥摆
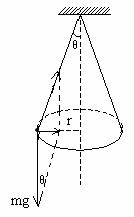
长度为 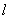 的细绳下端拴一个质量为m的小球,固定绳的上端,使小球沿水平面内的圆做匀速圆周运动。 的细绳下端拴一个质量为m的小球,固定绳的上端,使小球沿水平面内的圆做匀速圆周运动。
细绳转动恰好形成一个锥面,所以叫圆锥摆。
设绳与竖直方向成  角,球转动的角速度为 角,球转动的角速度为 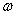 。 。
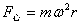  而 而 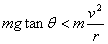
∴ 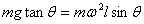 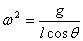
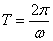 
当 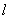 一定, 一定,  越大一定是 越大一定是 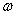 越大,T越小,即转得快。 越大,T越小,即转得快。
∴ 圆锥摆转动越快,悬线偏离竖直方向越多
(4)上述圆锥摆运动中若线速度忽然增大,则  增大,而 增大,而 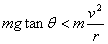 ,小球就要做离心运动使圆周运动半径增大。 ,小球就要做离心运动使圆周运动半径增大。
相反若速度 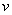 减小就要做近心运动,运动半径逐渐减小。 减小就要做近心运动,运动半径逐渐减小。
即外力小于向心力时就要做离心运动,外力大于向心力时就要做近心运动。
4. 应用匀速圆周运动规律求解问题的步骤和方法。
(1)确定研究对象
(2)找到运动过程中的状态变化,即从什么位置开始做圆周运动,要求的状态是否为圆周运动。
(3)对研究对象分析受力,尤其注重确定向心力方向。
(4)建坐标系原点在圆心,指向圆心为正方向,坐标轴随物体运动而运动。(转动的坐标系)
(5)由牛顿第二定律列方程。注重未知量个数,列方程个数。
注重:作用力,反作用力关系。
(6)解方程,进行必要的讨论。
【典型例题分析】
[例1] 匀速行进中的小车下面悬挂一个重物,若绳长为 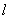 ,行进速度为v,当小车忽然刹车停止运动悬绳的拉力多大?(已知悬挂重物质量为m) ,行进速度为v,当小车忽然刹车停止运动悬绳的拉力多大?(已知悬挂重物质量为m)
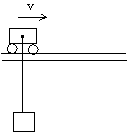
解析:小车匀速行进时,重物以相同的速度一起匀速前进,当小车紧急刹车而停止时,重物不能马上停止。以小车为圆心做圆周运动。重物受两个力,速度为v。
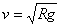 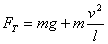 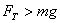
悬绳的拉力大小为 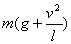
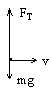
注重:小车停止后,重物不再做匀速直线运动,而是圆周运动。
[例2] 过山车是常见的刺激娱乐项目,可以简化为下面问题。竖直平面内的圆形轨道半径为R。过山车从倾斜轨道滑下进入圆形轨道,在竖直轨道上做圆周运动,求在圆形轨道最高点,车的最小速度。
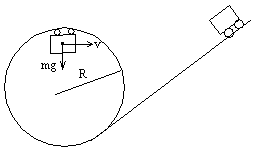
解析:过山车在圆形轨道做圆周运动轨道的支持力,重力的合力做向心力,车经最高点恰好不掉下来就是车没有离开圆轨道,又对轨道无压力,则 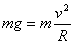
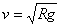 即过山车的最小速度至少为 即过山车的最小速度至少为 
当车速小于  ,重力大于向心力,车就要脱离轨道而掉下来。 ,重力大于向心力,车就要脱离轨道而掉下来。
当车速大于  则轨道的支持力与重力的合力做向心力,车对轨道有向上的压力。 则轨道的支持力与重力的合力做向心力,车对轨道有向上的压力。
[例3] 汽车与路面之间的动摩擦因数  ,转弯处弯道半径为 ,转弯处弯道半径为 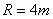 , ,  取 取  。 。
(1)若路面铺成水平的,汽车转弯时速度不能超过多大?
(2)若路面铺成外侧高内侧低的坡面,倾角为  ,汽车以多大速度转弯,与路面无摩擦。 ,汽车以多大速度转弯,与路面无摩擦。
(3)若是(2)中转弯路面,最大转弯速度是多少?
解析:路面是水平的,汽车转弯,向心力沿水平方向,摩擦力做向心力,速度最大摩擦也最大。
∴ 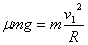
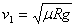 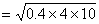 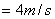
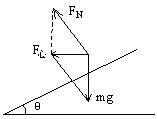
若弯路是坡面,且车与路面无侧向摩擦力
则 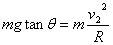 
(3)汽车以最大速度转弯则受三个力向心力沿水平方向,取水平方向为 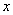 轴,竖直方向为 轴,竖直方向为  轴。 轴。
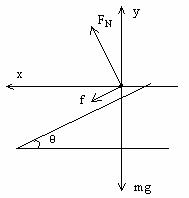
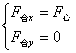 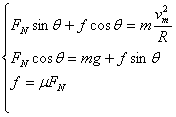
解得 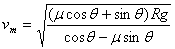 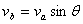 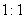
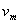 大于水平路面的最大转弯速度 大于水平路面的最大转弯速度
[例4] 质量为 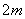 和 和  的小球分别固定在长为 的小球分别固定在长为 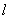 的轻杆两端。转杆绕过中点的水平轴匀速转动。若轻杆转动中对轴的作用力最小为零,求对轴作用力最大值。 的轻杆两端。转杆绕过中点的水平轴匀速转动。若轻杆转动中对轴的作用力最小为零,求对轴作用力最大值。
解析: 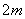 的球在最高点 的球在最高点 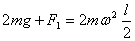 , ,  的球最低点 的球最低点 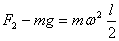 ,对轴的作用力 ,对轴的作用力  , ,  , , 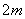 的球在最低点,对轴作用力 的球在最低点,对轴作用力  是最大值。 是最大值。

由题设知F最小为零
∴ 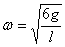 F最大值 F最大值 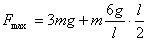 
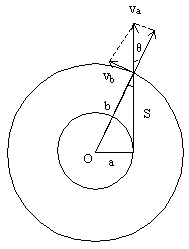
[例5] 如图所示,有一质量为m的小球P与穿过光滑水平板中心小孔O的轻绳相连,用力拉着绳的另一端使P在水平板上绕O点做半径为a的圆周运动,速率为 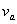 。若将绳忽然放松,然后再拉住,使小球到O点距离增大到b。 。若将绳忽然放松,然后再拉住,使小球到O点距离增大到b。
求:
(1)小球以b为半径做匀速圆周运动的速率
(2)小球运动由绳长为a到绳长为b的时间。
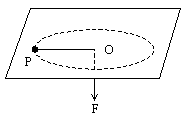
解析:小球绕O做圆周运动,绳忽然松开则无外力做向心力,球做离心运动沿切线S飞出,到绳长为b时受绳拉力速度改变,由于拉力沿绳的方向,小球速度 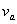 沿绳方向分速度减小为零垂直于绳的速度不变。当小球以b为半径做圆周运动速率就是 沿绳方向分速度减小为零垂直于绳的速度不变。当小球以b为半径做圆周运动速率就是 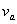 在垂直于绳的分量。 在垂直于绳的分量。
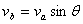 而 而 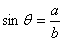 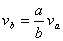
(2)运动S的时间 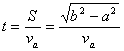
【模拟试题】
1. 甲、乙两个物体均做匀速圆周运动,甲的质量和轨道半径均为乙的一半,当甲转过
60°时,乙在这段时间里正好转过45°,则甲乙两个物体的向心力之比为 ( )
A. 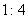 B. B. 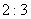 C. C. 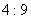 D. D. 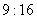
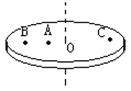
2. 以相同的材料做成的A、B、C三物体放在匀速转动的平台上,若都相对于平台静止,且 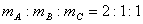 , , 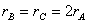 ,则( ) ,则( )
A. C的向心加速度最大
B. A受到的摩擦力最大
C. 转速增大时,C比B先滑动
D. 转速增大时,B比A先滑动
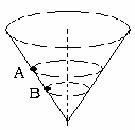
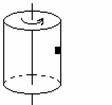
3. 一个内壁光滑的圆锥形筒固定在水平面上,如图所示。有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,A球运动的半径大于B球运动的半径,则( )
A. A球的角速度必小于B球的角速度
B. A球的线速度必小于B球的线速度
C. A球运动的周期必大于B球的运动的周期
D. A球对筒壁的压力必大于B球对筒壁的压力
4. 冰面上的溜冰运动员所受最大静摩擦力为运动员重力的K倍,在水平面上沿半径为R的圆周滑行的运动员,其安全速度为( )
A. v=K  B. v≤ B. v≤ 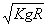
C. v≤  D. v≤ D. v≤ 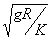
5. 如图所示,在光滑水平面上放一小球以某速度运动到A点,碰到一段半径为R的圆弧曲面AB,然后落到水平地面的C点,假如小球没有跟圆弧曲线上的任何点接触,则BC的最小距离为( )
A. 0 B. R C. 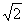 R D. ( R D. ( 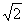 -1)R -1)R
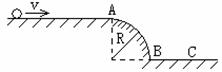
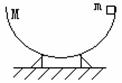
6. 如图所示,已知半圆形碗半径为R,质量为M,静止在地面上,质量为m的滑块滑到圆弧最底端速率为v,碗仍静止,此时地面受到碗的压力为( )
A. mg+m 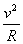 B. Mg+mg+m B. Mg+mg+m 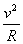
C. 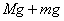 D. Mg+mg—m D. Mg+mg—m 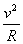
7. 如图所示,在光滑的以角速度ω旋转的水平细杆上,穿有质量分别为m和M的两球,两球用轻细线连接,若M>m,则( )
A. 当两球离轴距离相等时,两球相对杆不动
B. 当两球离轴距离之比等于质量之比时,两球相对杆都不动
C. 若转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动
D. 若两球相对杆滑动,一定向同一方向,不会相向滑动

8. 关于向心力的说法中正确的是( )
A. 物体受到向心力的作用才可能做圆周运动
B. 向心力是指向圆心方向的合力,是根据作用效果命名的
C. 向心力可以是重力、弹力、摩擦力等各种力的合力,也可以是其中某一种力或者某几种力的合力
D. 向心力只改变物体的运动方向,不改变物体的运动快慢
9. 两个做匀速圆周运动的物体,其质量之比为 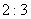 ,角速度之比为 ,角速度之比为  ,线速度之比为 ,线速度之比为 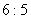 ,则它们的向心加速度之比为 ,它们所需向心力之比为 。 ,则它们的向心加速度之比为 ,它们所需向心力之比为 。
10. 一个做匀速圆周运动的物体,假如半径不变而速率增加到原来速率的3倍,其向心力增加了64N,那么物体原来受到的向心力的大小是 N。
11. 如图所示,物体与圆筒壁的动摩擦因数为μ,圆筒的半径为R。若要物体不滑下,则圆筒转动的角速度至少为 。
12. 地球在自转的过程中,质量为m、站在赤道上的人A和质量为2m、站在北纬  位置的人B,随地球一起转动,A和B随地球转动的角速度之比为 ,A和B随地球转动的线速度之比为 ,A和B随地球转动的向心加速度之比为 ,A和B随地球转动的向心力之比为 。 位置的人B,随地球一起转动,A和B随地球转动的角速度之比为 ,A和B随地球转动的线速度之比为 ,A和B随地球转动的向心加速度之比为 ,A和B随地球转动的向心力之比为 。
13. 用绳的一端拴一重物,手握绳的另一端使重物在竖直面内做圆周运动,试分析重物
到达最高点与最低点时向心力的来源,绳子在哪一点受到的拉力大?为什么?
14. 如图所示,高为h竖直圆筒内壁光滑,半径为R,顶部有入口A,在A的正下方处有出口B,一质量为m的小球自入口A沿切线方向水平射入圆筒内,要使球从B处飞出,小球进入入口A的速度应满足什么条件?在运动过程中,球对筒压力多大?
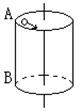
15. 如图所示,在光滑水平面上固定相距40cm的两个钉子A和B,长1m的细绳一端系着质量为0.4kg的小球,另一端固定在钉子A上,开始时小球和钉子A、B在同一直线上,小球始终以2m/s的速率,在水平面上做匀速圆周运动,若细绳能够承受最大拉力为4N,那么从开始到细绳断开所经历的时间是多少?
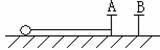
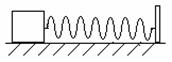
16. 如图所示,弹簧一端固定在转轴上,另一端与小物块相连,物块在光滑水平面上绕轴做匀速圆周运动,弹簧原长为0.5m,劲度系数为100N/m,物块质量为  kg,当物块转动周期为0.2s,弹簧的伸长量是多少? kg,当物块转动周期为0.2s,弹簧的伸长量是多少?
【试题答案】
1. C 2. D 3. AC 4. B 5. D 6. B 7. CD 8. ABCD
9. 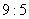 ; ; 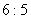 10. 8N 11. 10. 8N 11. 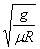 12. 12. 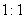 ; ; 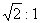 ; ; 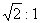 ; ; 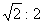
13. 略14. 小球速率  俯视小球做匀速圆周运动时间为t。A、B半径在同一方向, 俯视小球做匀速圆周运动时间为t。A、B半径在同一方向, 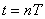 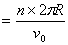 竖直方向小球做自由落体运动, 竖直方向小球做自由落体运动, 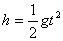 , , 
 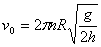 向心力 向心力 
15. 设小球恰好断开时,运动半径为 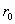 , ,   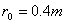
小球绕第三个半周时半径为  ,所以当小球绕完两半周接第三个半圆时绳子断开。时间为 ,所以当小球绕完两半周接第三个半圆时绳子断开。时间为 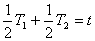 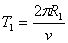 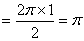  
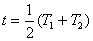 
16. 设伸长量为 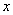 。 。 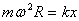 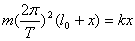
 解得 解得 
|