|
匀变速直线运动的研究(复习)
★新课标要求
1、通过研究匀变速直线运动中速度与时间的关系,位移与时间的关系,体会公式表述和图象表述的优越性,为进一步应用规律奠定基础,体会数学在处理问题中的重要性。通过史实了解伽利略研究自由落体所用的实验和推论方法,体会科学推理的重要性,提高学生的科学推理能力。
2、在把握相关规律的同时,通过对某些推论的导出过程的经历,体验物理规律“条件”的意义和重要性,明确很多规律都是有条件的,科学的推理也有条件性。
★复习重点
匀变速直线运动的规律及应用。
★教学难点
匀变速直线运动规律的实际应用。
★教学方法
复习提问、讲练结合。
★教学过程
|
应用:①判定运动性质(匀速、变速、静止)②判定运动方向(正方向、负方向)③比较运动快慢④确定位移或时间等 |
|
应用:①确定某时刻的速度②求位移(面积)③判定运动性质④判定运动方向(正方向、负方向)⑤比较加速度大小等 |
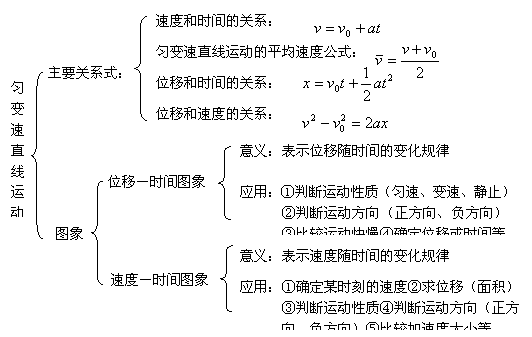 (一)投影全章知识脉络,构建知识体系 (一)投影全章知识脉络,构建知识体系
|
定义:在同一地点,一切物体在自由落体运动中的加速度都相同,这个加速度叫做自由落体加速度 |
|
数值:在地球不同的地方g不相同,在通常的计算中,g取9.8m/s2,粗略计算g取10m/s2 |
|
注重:匀变速直线运动的基本公式及推论都适用于自由落体运动,只要把v0取作零,用g来代替加速度a就行了 |
(二)本章复习思路突破
Ⅰ 物理思维方法
l、科学抽象——物理模型思想
这是物理学中常用的一种方法。在研究具体问题时,为了研究的方便,抓住主要因素,忽略次要因素,从而从实际问题中抽象出理想模型,把实际复杂的问题简化处理。如质点、匀速直线运动、匀变速直线运动、自由落体运动等都是抽象了的理想化的物理模型。
2、数形结合思想
本章的一大特点是同时用两种数学工具:公式法和图象法描述物体运动的规律。把数学公式表达的函数关系与图象的物理意义及运动轨迹相结合的方法,有助于更透彻地理解物体的运动特征及其规律。
3、极限思想
在分析变速直线运动的瞬时速度时,我们采用无限取微逐渐逼近的方法,即在物体经过的某点后面取很小的一段位移,这段位移取得越小,物体在该段时间内的速度变化就越小,在该段位移上的平均速度就越精确地描述物体在该点的运动快慢情况。当位移足够小时(或时间足够短时),该段位移上的平均速度就等于物体经过该点时的瞬时速度,这充分体现了物理中常用的极限思想。
Ⅱ 高考趋向分析
本章内容是历年高考的必考内容。近年来高考对本章考查的重点是匀变速直线运动的规律及图象。对本章知识的单独考查主要是以选择题、填空题的形式命题,没有仅以本章知识单独命题的计算题,较多的是将本章知识与牛顿运动定律、电场中带电粒子的运动等知识结合起来进行考查。
Ⅲ 解题方法技巧及应用
1、要养成根据题意画出物体运动示意图的习惯,非凡对较复杂的运动,画出图可使运动过程直观,物理图象清楚,便于分析研究。
2、要注重分析研究对象的运动过程,搞清整个运动过程,按运动性质的转换,可分为哪几个运动阶段,各个阶段遵循什么规律,各个阶段间存在什么联系。
3、由于本章公式较多,且各公式间有相互联系,因此,本章的题目常可一题多解,解题时要思路开阔,联想比较,筛选最简捷的解题方案。解题时除采用常规的解析法外,图象法、比例法、极值法、逆向转换法(如将一匀减速直线运动视为反向的匀加速直线运动)等也是本章解题中常用的方法。
(三)知识要点追踪
Ⅰ 匀变速直线运动规律应用
1、匀变速直线运动的规律
实质上是研究做匀变速直线运动物体的初速度v0、末速度v、加速度a、位移x和时间t这五个量的关系。具体应用时,可以由两个基本公式演绎推理得出几种非凡运动的公式以及各种有用的推论,一般分为如下情况:
(1)从两个基本公式出发,可以解决各种类型的匀变速直线运动的问题。
(2)在分析不知道时间或不需知道时间的问题时,一般用速度位移关系的推论。
(3)处理初速为零的匀加速直线运动和末速为零的匀减速直线运动时,通常用比例关系的方法来解比较方便。
2、匀变速直线运动问题的解题思想
(1)选定研究对象,分析各阶段运动性质;
(2)根据题意画运动草图
(3)根据已知条件及待求量,选定有关规律列出方程,注重抓住加速度a这一要害量;
(4)统一单位制,求解方程。
3、解题方法:
(1)列方程法(2)列不等式法(3)推理分析法(4)图象法
Ⅱ 巧用运动图象解题
运动图象(v-t图象、x-t图象)能直观描述运动规律与特征,我们可以用来定性比较、分析或定量计算、讨论一些物理量。
解题时,要非凡重视图象的物理意义,如图象中的截距、斜率、面积、峰值等所代表的物理内涵,这样才能找到解题的突破口。
(四)本章专题剖析
[例1]一物体以初速度v1做匀变速直线运动,经时间t速度变为v2求:
(1)物体在时间t内的位移.
(2)物体在中间时刻和中间位置的速度.
(3)比较vt/2和vx/2的大小.
【解析】 (1)物体做匀加速直线运动,在时间t内的平均速度 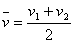 , ,
则物体在时间t内的位移
x= 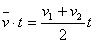
(2)物体在中间时刻的速度
vt/2=v1+a·  ,v2=v1 at,故 ,v2=v1 at,故
vt/2= 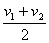 . .
物体在中间位置的速度为vx/2,则
由①②两式可得vx/2= 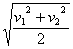
(3)如图所示,物体由A运动到B,C为AB的中点,若物体做匀加速直线运动,则经  时间物体运动到C点左侧,vt/2<vx/2;若物体做匀减速运动,则经 时间物体运动到C点左侧,vt/2<vx/2;若物体做匀减速运动,则经  时间物体运动到C点右侧,vt/2<vx/2,故在匀变速直线运动中,vt/2<vx/2 时间物体运动到C点右侧,vt/2<vx/2,故在匀变速直线运动中,vt/2<vx/2
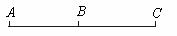
【说明】匀变速直线运动的公式较多,每一问题都可以用多种方法求解,解题时要注重分析题目条件和运动过程的特点,选择合适的公式和简便的方法求解.
[例2]特快列车甲以速率v1行驶,司机忽然发现在正前方距甲车s处有列车乙正以速率v2(v2<v1)向同一方向运动.为使甲、乙两车不相撞,司机立即使甲车以加速度a做匀减速运动,而乙车仍做原来的匀速运动.求a的大小应满足的条件.
【解析】 开始刹车时甲车速度大于乙车速度,两车之间的距离不断减小;当甲车速度减小到小于乙车速度时,两车之间的距离将不断增大;因此,当甲车速度减小到与乙车速度相等时,若两车不发生碰撞,则以后也不会相碰.所以不相互碰撞的速度临界条件是:
v1-at = v2 ①
不相互碰撞的位移临界条件是
s1≤s2+s ②
即v1t- 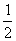 at2≤v2t+s ③ at2≤v2t+s ③
由①③可解得 a≥ 
【说明】 (1)分析两车运动的物理过程,寻找不相撞的临界条件,是解决此类问题的要害.
(2)利用不等式解决物理问题是一种十分有效的方法,在解决临界问题时经常用到.
[例3]一船夫驾船沿河道逆水航行,起航时不慎将心爱的酒葫芦落于水中,被水冲走,发现时已航行半小时.船夫马上调转船头去追,问船夫追上酒葫芦尚需多少时间?
【解析】 此题涉及到船逆水航行、顺水航行两种情况, 并且有三个不同速度:u——水速、(v-u)——船逆水航速、(v u)——船顺水航速.虽然都是匀速直线运动但求解并不很轻易.该题假如变换参考系,把参考系在顺水漂流的葫芦上,则极易看到,船先是以船速离去, 半小时后又原速率返回.
取葫芦为参考系,设船远离速度为v,则s = vt1,式中s为船相对葫芦的距离,t1为远离所用时间.
设船返回并追上葫芦所需时间为t2,由于船相对葫芦的速度仍然是v,故
s=vt2易得t1=t2.
【说明】由于物体的运动是绝对的,而运动的描述是相对的,所以当问题在某参考系中不易求知,变换另一个参考系进行研究常可使问题得以简化,其作用在此题中可见一斑.
[例4]跳伞运动员做低空跳伞表演,他在离地面224 m高处,由静止开始在竖直方向做自由落体运动.一段时间后,立即打开降落伞,以12.5 m/s2的平均加速度匀减速下降,为了运动员的安全,要求运动员落地速度最大不得超过5 m/s(g取10 m/s2).
(1)求运动员展开伞时,离地面高度至少为多少?着地时相当于从多高处自由落下?
(2)求运动员在空中的最短时间是多少?
【解析】 (1)设运动员做自由落体运动的高度为h时速度为v,此时打开伞开始匀减速运动,落地时速度刚好为5 m/s,这种情况运动员在空中运动时间最短,则有
v2=2gh ①
vt2-v2=2a(H-h) ②
由①②两式解得h=125 m,v=50 m/s
为使运动员安全着地,他展开伞时的高度至少为H-h=224 m-125 m=99 m.
他以5 m/s的速度着地时,相当于从h′高处自由落下,由vt2=2gh′
得h′=  m=1.25 m m=1.25 m
(2)他在空中自由下落的时间为
t1= 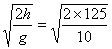 s=5 s s=5 s
他减速运动的时间为
t2= 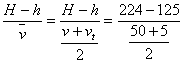 m/s=3.6 s m/s=3.6 s
他在空中的最短时间为
t=t1+t2=8.6 s
(五)课堂练习
1.几个做匀变速直线运动的物体,在t s内位移最大的是
A.加速度最大的物体 B.初速度最大的物体
C.末速度最大的物体 D.平均速度最大的物体
2.若某物体做初速度为零的匀加速直线运动,则
A.第4 s内的平均速度大于4 s内的平均速度
B.4 s内的平均速度等于2 s末的瞬时速度
C.第4 s内的速度变化量大于第3 s内的速度变化量
D.第4 s内与前4 s内的位移之比是7∶16
3.一物体由静止沿光滑斜面匀加速下滑距离为l时,速度为v,当它的速度是v/2时,它沿斜面下滑的距离是
A.l/2 B. 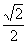 l C. l C.  l D. l D.  l l
4.A、B、C三点在同一直线上,某物体自A点从静止开始做匀加速直线运动,经过B点的速度为v.到C点的速度为2v,则AB与BC两段距离大小之比是
A.1∶4 B.1∶3
C.1∶2 D.1∶1
5.一辆汽车做匀速直线运动,在5 s内通过相距50 m的A、B两根电线杆,若汽车经过B杆后改做匀加速直线运动,到达下一根电线杆时速度达到15 m/s,若B、C两杆相距也是 50 m,则此汽车的加速度是______ m/s2.
6.物体做匀变速直线运动,它的初速度是1 m/s,在第1 s内的平均速度是15 m/s,它在第6 s内的平均速度是______ m/s.
7.一物体做匀变速直线运动,在第3 s内的位移是15 m,第8 s内的位移是5 m,则物体的初速度为______,加速度为______.
8.一滑块由静止从斜面顶端匀加速下滑,第5 s末的速度是6 m/s,求:
(1)第4 s末的速度;
(2)前7 s内的位移;
(3)第3 s内的位移.
参考答案
1.D 2.ABD 3.C 4.B
5.1.25(提示:vB= 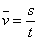 vC2-vB2=2as) vC2-vB2=2as)
6.6.5(提示: 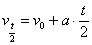 (t=1 s),故a=1 m/s2, (t=1 s),故a=1 m/s2, 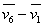 =aΔt,Δt=5 s) =aΔt,Δt=5 s)
7.20 m/s;-2 m/s2(提示:利用平均速度求解)
8.解:(1)由v=at得a=v/t= 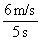 =1.2 m/s2 =1.2 m/s2
所以v4=at4=1.2×4 m/s=4.8 m/s
(2)前7 s内的位移
s1= 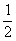 at2= at2= 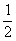 ×1.2×72 m=29.4 m ×1.2×72 m=29.4 m
(3)第3秒内的位移:
s2= 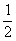 at32- at32- 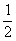 at22= at22= 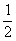 a(t32-t22)= a(t32-t22)= 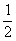 ×1.2×(9-4) m=3 m ×1.2×(9-4) m=3 m
★课余作业
复习本章内容,预备章节过关测试。
|