有趣的平面镜问题

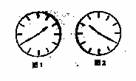题1：如图1所示是从竖直放置的平面镜中看到的钟表的像，你知道此时的实际时间是多少吗?

解：下面我们从五种不同的方法进行分析：

1、由于物像对称，故钟表在平面镜里成像后将左右调换， 将钟表沿6点和12点之间平分后，左右对称，可知，此时时间为10时20分，如图2.

2、将纸翻过来，从背面透过纸观察，此时指针所指时刻为10 时20分。

3、沿逆时针方向读数，先读时针为10时，再读分针为20分。

4、先直接读数为1时40分，再用12时减去1时40分， 则实际时间为10时20分。

5、用一平面镜使钟表再成一次像，通过平面镜可直接读数。

题2：哪些大写英文字母，经过平面镜成像后，仍然为原来的字母？

解：这些字母有A、H、I、M、O、T、U、V、W、X、Y。

题3：检查视力时，眼与视力表应相距5米远， 若房间两墙壁间的距离只有3米，你有什么办法呢?

\s 解：可在墙壁上挂一视力表，在对面墙壁的同一高度挂一平面镜， 被检者面对平面镜，与镜相距2米， 那么视力表在平面镜中的像与被检者之间的距离就是5米了。如图3.

题4：假如某人身高为1.8米，他要想在平面镜中观察到自己的全身像，则这个平面镜至少要多长?

解：如图4所示，从B点发出的光线经平面镜反射后， 射入人的眼睛，人眼逆着反射光线就可看到人脚，由几何知识和反射定律可知，此时MN= 1/2AB，镜子至少需要0.9米

题5：在两个平行的平面镜前放置一个小泥人， 此时这个镜子里将有多少个像。

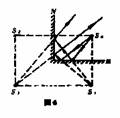
\s 解：这里平面镜内将有无数个像.，如图5所示，从S0发出的光经平面镜M1，成像在S1位置，S1经平面镜M2成像在S2位置，…… 依次类推，可成无数个像。

题6：在两个竖直放置的平面镜前有一根点燃的蜡烛， 问此时人眼能同时观察到几根蜡烛的像，假如夹角为60°，30°呢?

解：如图所示，S1和S2是关于平面镜M、N成的像.假如S发出的光线连续经过两平面镜反射，则人眼将观察到像点S3，故可观察到3个像。 假如平面镜夹角为60°、30°，则成像个数为360°/60°—1 =5个； 360°/30°—1=11个

题7：如图7，小明在一竖直放置的偶像面前(两平面镜成90 °夹角)，眨了一下左眼，则镜中的像是眨左眼，还是右眼呢?

解：眨右眼，因为此时的成像情况与平面镜成像不同， 左半部分脸成像在右边，右半部分脸成像在左边。

题8：在十字路口，耸立着豪华的大楼，它临街的一面全部都是新型的玻璃装饰，因此， \s 过往的车辆都在这面大的平面镜中成像， 如图8所示，小刚在十字路口中心，面向北而立，从这面镜子中看到一辆汽车向东行，驶到十字路口，向左转弯，这辆汽车实际上是在向哪行驶?往哪转弯?

解：向北行驶，向右转弯

题9：小明理发后，很想看看自己的后脑部理得怎样，他想了想，便利用所学的光学知识将两面镜子配合比试后，终于看到了自己的后脑勺，你知道他是怎样设计的呢?

解：如图9所示，他把第一面镜子L1面对自己，第二面镜子L2放在后脑勺旁边，光线经平面镜成像后，可进入小明眼中。

题10：在江边观察节日的夜景时，经常会看到对岸江边屋檐边上的电灯，在江中的像不是一盏电灯而是一条光柱，这是为什么呢?

解：这是由于江面发生漫反射电灯光成像的结果，由于水面总有水波起伏，好象由许多取向不同的平面镜组成的一样，电灯在每一个平面镜内都成一个像，但各个像的位置高低不同，这些像组合起来就形成了一条光柱。

1吨木头和1吨铁，哪一个重？

1吨木头和1吨铁，哪一个重？这还不知道，一样重。可是假如有人回答说：“1吨木头重。”你一定会大笑起来。然而，严格地讲，这个答案才是正确的！

因为平常我们说的1吨铁和1吨木头，是指铁和木头在空气里称起来的重量。假若有一架很大的天平，我们把这堆铁和这堆木头分别放在天平的两盘上，那么，它们在空气里称得的结果是正好平衡的。

但是，我们都有知道，任何物体放在空气里都要受到浮力的作用。因此一个物体的真正重量，应该是它在真空里称出来的重量。可是我们平常所指的重量，都是在空气里称出来的。既然是在空气里称的，就要受到空气的浮力作用，所以它的重量就要减小。根据阿基米得原理，物体在空气里所受的浮力，等于这个物体所排开的空气的重量；也就是说，在空气中称得的重量，等到于物体的真实重量减去物体所受的浮力。

此题中，木头的体积比铁的体积大，所以木头所受的浮力大于铁的浮力，因此，木头的真正重量，应该等于1吨重加上木头所受的浮力；而铁的真正重量，应该等于1吨重加上铁所受的浮力。

1吨铁大约占八分之一立方米的体积，1吨木头约占2立方米。它们的浮力相差约2.3千克力。所以1吨木头的真正重量，就比1吨铁的真正重量约重2.3千克。

“数液滴法”测密度

一个外形不规则的石腊块、两个玻璃杯、足量的水、细线、针、一个长约20厘米的用在自行车气门芯上的软胶管。你有什么办法测出石蜡的密度？

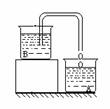方法：1、在玻璃杯A中注满水，用细线拴上石腊，使其漂浮在水中，这时杯A中要溢出一部分水。接着将石腊从水中提出来，将另一玻璃杯B垫高，并倒入一定量的水。然后，利用虹吸现象将玻璃杯B中的水通过软胶管引出来，一滴滴地流入A中，如图。直到将杯A注满为止，记下水滴数n1。（实验前，最好先试滴几次，可通过调节出水管口的高度，从而控制水流的速度，使水一滴一滴的滴下来。）

2、用针将石腊按住，使其浸没在玻璃杯A中，此时A杯中 有水溢出。接着用细线将石腊提出来，用同样的方法（保持同样的水流速度），将A杯注满水，并数出水滴数n2。

3、设石腊的密度为ρ0，体积为V蜡，水的密度为ρ水，石蜡排开水的体积是V水 。当石腊漂浮在水面时，根据阿基米德定理，得： ρ0gV蜡=ρ水gV水。 由于每滴水的体积可以认为是相同的，所以可以得出V蜡/V水=n2/n1，因此，石腊的密度ρ=ρ水·n1/n2

如何测蜡块的体积

题：测一个不规则外形的蜡块的体积，你能想出多少种方法呢？要求，方法尽可能多，测量方法要合理。

　　方法一：用“排液法”测出蜡块的体积。由于蜡块的密度比水小， 因此可以采用“按压法”或“沉锤法”。

　　方法二：还是采用“排液法”。这时， 可直接找一个密度比蜡块小的液体来测量，如利用酒精等。

　　方法三：利用“排沙法”开始往量筒内装一定量的沙， 测出沙的初始体积，然后再将蜡块浸没在这些沙中，测出沙与蜡块的总体积， 从而算出石蜡的体积。

　　方法三：利用“查表法”。先用天平测出蜡块的质量， 再从密度表中测出石蜡的密度，从而算出石蜡的体积。

　　方法四：利用“变形法”。将蜡块熔化后，倒入一个规则器皿内， 等凝固后取出，用刻度尺算出体积。

　　方法五：利用“比例法”。先用天平测出蜡烛的总质量Ｍ， 然后用小刀把蜡块切成一个规则物体，测出长、宽、高算出体积Ｖ0， 接着用天平测出规则物体的质量ｍ0，最后根据公式Ｖ＝ＭＶ0/ｍ0。

方法六：利用“溢水法”。找一个溢水杯，装满水， 将石蜡按入水中，使水溢出，并用量筒接住， 读出量筒内水的体积就行了；也可把溢出的水用烧杯接住，用天平设法测出溢出水的质量，从而计算溢出水的体积， 此体积即为石蜡的体积。

用数学思想解答一道物理题

例：在水平桌面上有一叠圆形金属片，最下面一块的重力为G，面积为S，它相邻的上面一块金属片重G/2，面积为S/2，……。如此类推，即金属片的重力和面积逐渐减半，一直叠下去。求每块金属片下表面所受压强之比为多少?

解析：依题意，从下往上数，每块金属块的重力分别为：G、G/2、G/4、G/8、……G/2n，此题如用无穷等比数例公式求解，显然很好，但由于初中生没有学过这一数学知识，因此，我们可以从一古代数学思想入手，巧妙地解答此题。

我国古代数学中曾有“一尺之棰，日取一半，万世不竭”的说法，它的意思是：一尺长的木棒，假如天天取前一次的一半扔掉，那么永远也不可能将它分完。显然，假如把扔掉的木棒全部合在一起，其数值应该为1，根据这一思想，我们不难得出，桌面所受重力为：

G G/2 G/4 G/8 …… G/2n=2G

第一块金属的上表面所受总重力为：

G/2 G/4 G/8 …… G/2n=G

依次类推，第二块、第三块的上表面所受重力为：

G/4 G/8 …… G/2n=G/2

G/8 G/16 …… G/2n=G/4

……………………………

而从桌面往上，各金属块下表面的面积依次为

S、S/2、S/4、S/8…… S/2n

因此，各金属块下表面所受压强应为：2G/S。

即各金属块所受压强之比为1：1：1：……1。

不估不知道，一估吓一跳

题1：估一估，你大拇指指甲上所受的大气压大约为多大？相当于1根鸡毛重？一支钢笔重？还是几斤酒重？

解：人体大拇指的面积约为1厘米2左右，大拇指所受的大气压强约为P0=1.01×105帕，则大拇指上所受的压力约为：F=P0S≈1.01×105帕×1×10-4米2≈10牛

小小一个大拇指表面上承受的力约为1千克力，相当于一对礼品酒吊在你的大拇指上。你说大不大!

题2：假如把你雕成一个等大的石像，花费的石料约为M0千克，现在需要重塑这个石像，使它的身高变为原来的2倍， 那么这时所花费的石料应是原来的几倍？2倍？4倍？还是8倍？

解：由于身高变为原来的2倍，则其长和宽也应变为原来的2倍， 故其总体积应变为原来的8倍，所以这时花费的石料是原来的8倍！你猜对了吗？

题3：你来到这个世界后，始终“霸占”着一定的空间，假如某一天，你“脱胎升仙”了，那么你所“腾让”出来的这个空间， 所装的空气为多重呢？显然，这个重力就是你每时每刻都受到的一个浮力 ，它相当于一根大头针重？一个鸡蛋重？还是一瓶酒重？

解：根据F浮=ρ空气gV排.

而V排= m人/ρ人

又∵ρ人与ρ水大致相等，故：F浮=ρ空气g× m人/ρ水

m人=50千克，代入数据可得：F浮 = =0.65牛

0.65牛顿相当于一个鸡蛋的重力，你猜对了吗？

题4：假如把教室内的空气放在一个特制的大天平的左盘内， 让你站在天平的右盘，请你猜猜哪边重？

解：估计教室的长为10米，宽为6米，高为3米，则根据F空=ρ空·gV排=(1.29×10×3×6×10)牛=2322牛

大约相当N个中学生的重力，则N= 2322牛/500牛 ≈5个

你必须喊上你的四个同伴，才能和教室内的空气配重!

题5：大象的重力可达6.0×103千克，鲸的重力可达1.5×10 5千克，它们各是你的重力的多少倍？

解：一头大象相当于N1个中学生的重，一头鲸相当于N2个中学生的重，则

N1= 6.0×103千克/50千克 =120倍

N2=1.5×105千克/ 50千克=3000倍

一头大象居然相当于2～3个班的中学生的总重量，一头鲸居然相当于1～2个学校的总人数的重量。

题6：冬天洗脸的时候，一盆热水所释放的热量，估计可以把你举高多高。

解：假设一盆水有2千克，水的初温为70℃，末温为10℃， 人的质量约为50千克，g取10牛/千克。

则根据 Q放=W可知： Cm水△t=m人gh

h= Cm水△t /m人g =2×(70-10)×4.2×103 / 50×10米 ≈1千米

小小一盆水所放出的热量居然可以把你举高1千米左右!

一滴水也能浮起一头牛

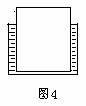
我们先看这样一个问题：“1N的水能托起10N重的物体吗? ”很多同学可能要回答：不能。他们是这样理解的，因为1 牛的水即使全部被排完，也只能产生1牛的浮力，因浮力小于重力，故物体不可能上浮。

我们不妨这样设想，设容器中装有11N重的水，有一重10N的物体（密度比水小）放入容器中，这时，它浮在水面上，此时，排开的水为10N， 容器内只剩下1N的水了，可见1N的水完全可以托起10N的重物。

在这里“排开”的水重是10N，而不是1N，其V排的含义应是图中物体浸没在水下的体积，而不是周边水的体积。因此，1N的水最多能浮多重的物体是不确定的。从理论上讲，一滴水完全可以浮起一头牛。

杠杆越长越省力吗?

大家知道，阿基米德曾有过这样的豪言壮语： “给我一个立足点和一根足够长的棍，我就能撬动地球。”可是，在一次保卫叙拉古城的时候 ，他却冲几名正在用杠杆搬动石头的士兵大声喊道： “不要用那么长的杠杆，换一根短的。”将士们都惊呆了，用短杠杆怎么行? 您发明的杠杆原理不是要加长动力臂才省力吗? 遗憾的是由于城堡被敌人攻破，阿基米德还来不及回答将士们的问题，就被罗马士兵杀害了。

这个传说是否真实，我们不必考虑，但是我们关心的是杠杆是不是越长越好呢?通过下面的例题，我们来分析这个问题。

例：如图1所示，有一杠杆，每米长重为40牛顿，可绕O点转动，要将距支点0.5米处的，一个重为490牛的石头撬动，问杠杆应为多长时，作用在杠杆另一端的力最小。

分析和解：设杠杆长为L，则此杠杆的支点为O，A端的力F1为动力，动力臂为L；阻力有两部分：杠杆自身重G=L×40牛，其力臂为L/2；被撬石头对杠杆B点的压力F2=490牛，力臂为OB=0.5米。

由杠杆平衡原理可得：F1L=40L×L/2 490×0.5

F1=20L 245/L

根据数学知识可知：

当20L=245/L时F1有极小值。

解之可得：当L=3.5米时，

F1极小=140牛 图 1

由此可见，杠杆最省力时，其长度为3.5米，而当杠杆大于或小于3.5米时，所用的力都要大。可见阿基米德所说的话还是有一定道理的。

三个和尚有水吃

小明看了故事片“一个和尚挑水吃，二个和尚抬水吃，三个和尚没水吃”以后，想利用自己学过的杠杆知识为他们排忧解难，不一会，他就设计了一种方案，他利用了两根等长的扁担，几段绳子， 使三个和尚抬水的时候，每个人肩上都承担了相同的重力，这样三个和尚再也没有斤斤计较了，你知道他采用的是什么方案吗?

对了，他采用图1所示的方法解决的，他把扁担CD系在AB的中点，在离C点为2/3CD的位置E点系上木桶，这样，甲、乙、丙三个和尚分别抬住A、B、C三点，其承担的力都为桶重的1/3，你知道这是为什么吗?

我们不妨先分析杠杆CD的受力情况，假如选D点为支点，则E、C两 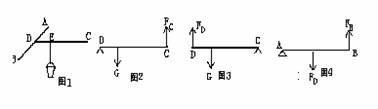点受力情况如图2所示，根据杠杆平衡原理可知， 则FC==G/3。假如选C点为支点，则E、D两点受力如图3所示， 由杠杆平衡原理可得：FD=2G/3。再分析AB棒所受力，假如选A点为支点，则D点、B点受力如图4所示，则FB=FD/2=G/3，。同理，假如选B点为支点，则A点所受力应为FA=G/3。

通过以上分析可知FA=FB=FC=G/3

究竟谁吃亏

小卓、小越在一本杂志上，看到了这样一个故事：

一次，检查员发现某药店的一台天平左右两臂不相等，于是责令营业员停止使用该天平，但这时却刚好跑进来一顾客，要求购买200克药品， 营业员急中生智地对检查员说：我先在左盘里放药品，右盘放100克砝码， 然后再在左盘放100克砝码，右盘放药品，这样一次药品的质量多于100克，一次药品的质量少于100克，两次扯平了，刚好200克，这样，谁也不吃亏。

小越看后，不加思考地说：营业员说得有道理，这样谁也不吃亏。

小卓却摇摇头说：那可不一定，我们还是来推理一下吧!

我们设天平的两个力臂分别为L1、L2，设第一次所放的药品质量为m1，第二次所放的质量为m2，则根据杠杆平衡原理可得：m1l1=O.1 l2 (1)

0.1l1=m2l2 (2)

由(1)÷(2)得 m1m2=0.12

又因为天平两臂不等 ，所以m1≠m2

即(√m1-√m2)2＞0，化简m1＋m2＞2√m1m2=0.2(千克)

即营业员前后两次称量的总和要大于0.2千克，所以营业员要吃亏。

小越听完后，连连点头：“有道理，有道理，我怎么没想到!”

几则有趣的杠杆题

以下几道杠杆题十分有趣，请同学们根据题意判定一下杠杆是否平衡。

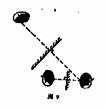
1、如图，天平左盘中有一个已被抽成真空的玻璃瓶，与瓶相连的橡皮管的上端通过一段玻璃管接一个吹起的气球， 气球与玻璃瓶之间被夹在橡皮导管上的铁夹隔断， 在天平右盘中加有砝码，使天平处于平衡状态，当把铁夹打开后，天平还平衡吗?

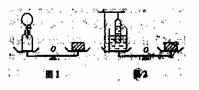解析：找开夹子后，气球中的气体将进入瓶中一部分， 因而气球的体积减小，空气对它的浮力也随之减小，使得天平的左端下沉。

2、如图2所示，左盘内是一个托里拆利实验装置，但支架支在左盘内，此时天平平衡，则当大气压增加时，天平将( )

解析：当大气压强增加时，槽内水银将被吸入托里拆利管中，使管内水银增重，此时，虽然水槽对左盘的压力减小，但支架对左盘的压力却增加了， 其增加量和减小量相等，故天平仍然平衡。

3、如图3所示，一把均匀直尺可以绕中点O自由转动， 直尺上有三只垂直而立的蜡烛A、B、C，它们的粗细、材料和燃烧速度均相同。但长度关系为LA=LB=LC/2，此时杠杆平衡，在杠杆燃烧的过程中， 直尺将( )

解析：假设A、B已燃尽，此时C还有一半没燃完，故此时左端要下沉。

4、如图4所示，有一轻质杆AB支于O点， 在其两端分别挂有质量不计的小桶，当桶内分别装有一定质量的沙时，恰好平衡，此时AO>OB。假如此时分别在两小桶底部开一相同大小的孔，让沙缓缓流出，且每秒从两桶中流出的沙的质量相等，则杠杆将( )

解析：因为AO>OB，所以左端桶内的沙质量较少。现同时流沙， 假设1秒内左桶全部流完，而此时右桶还有剩余， 故此时杠杆左端将上升。

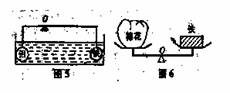5、如图5所示， 一不等臂的轻质杠杆两端分别挂一实心铁球和一实心铝球，浸没在水中时，杠杆刚好平衡，若往水中加盐，则杠杆( )

解析：假设加盐后，其密度可增到2.7×103千克/米3，此时铝球将悬浮在液体中，而铁球由于密度相对较大，故要下沉， 故若往水中加盐，杠杆将左端下沉。

6、如图6所示，在一密闭的玻璃容器内，有一天平两端放有等质量的棉花和铁块，今将玻璃容器抽成真空，则天平将( )

解析：在空气中，由于棉花体积大，故所受浮力大，现在玻璃容器抽成真空， 其浮力为0，即棉花的浮力减小得较多，故棉花一端将下沉。

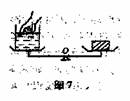
7、如图7所示，天平左盘容器内盛有适量的水，此时天平平衡，假如将一食指插入液体中，但不碰到容器壁和容器底，则天平将( )

解析：食指虽没碰到容器壁和底，但它排开了一定的体积，因此，受到了一定的浮力，既然有浮力，就有浮力的反作用力， 即手对水的压力，因此左盘下沉。(此题也可根据水位上升，压强增大，压力增大来判定)。

悬涯峭壁遇难题 杠杆原理显神通

\s 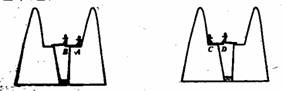小卓、小越是一对双胞胎。今天刚一放暑假， 兄弟俩就预备到对面山上的外婆家去度假，可是走在半路上，他们发现，在到外婆家的路上有一个悬崖 ，悬崖上原来的木桥因天长日久，已经腐化，不复存在了。这可怎么办？兄弟俩只得四处寻找东西，希望能找到一个合适的材料，搭桥过去。真巧！他俩在一个破旧的房子里找到了两块木板，兄弟高兴奋兴的扛到悬崖边，一试，不行！两块木板都不够长，就差那么一丁点！兄弟俩又急忙找绳子，这回可不那么幸运了，什么也找不到。这可怎么办？你能帮他们想个办法吗?

对了，利用杠杆原理就可成功， 我们先将其中的甲木板的三分之一露在悬崖上，小卓站在甲木板的A端，小越扛着乙木板走到甲木板的B端，将乙木板搭在B点和对岸之间，顺利的通过悬崖。然后小越再将乙木板拉回， 只让三分之一露出悬崖，小越站在C端，小卓将甲木板搭在乙木板上，然后通过甲木板，当小卓走到乙木板上的D点时，小卓将甲木板收起，扛到对岸，兄弟俩就顺利通过了这道悬崖。

请你思考一个问题：在第一幅图中，我们知道小卓离支点的距离为2/3的板长，假如小越向前走以后，离支点的距离超过了2/3，那么杠杆会不会失去平衡？对了，不会失去平衡，因为这时是两根杠杆，而不是一根杠杆，假如你对两根杠杆分别进行分析，你会发现，他们其实是很安全的。

阿基米德能举起地球吗?

阿基米德曾经对叙拉古的国王说：“给我一个立足点和一根足够长的棍， 我就能搬动地球”。国王一听感到非常吃惊，心想阿基米德是不是病了， 胆敢夸这么大的海口， 于是他命令阿基米德去移动放在海边陆地上的一条大船。阿基米德叫工匠在船的前后左右安装了一套设计精巧的滑轮和杠杆，并让国王牵动一根绳索， 船就慢慢地移到了海里。国王见此情形，十分钦佩，当众公布：“从现在起，我要求大家，无论阿斯米德说什么，都要相信他！”阿基米德的确用较小的力就产生了较大的力，但是假如真让他去搬动地球，他行吗？

让我们设想阿基米德真的找到了一个立足点， 再设想他真的找到了一根足够长的杠杆， 你知道他假如把地球哪怕只举起一厘米，得用多长时间吗？──至少要用三十万万万年。

即使阿基米德的手能够运动得和自然界最大的光速一样快， 他也只能在做了十几万年的工作以后，才能把地球举起一厘米。

再者，我们知道地球的质量是６×１０24千克，那么，地球的重力就是６×9.8×１０24牛吗？否，因为重力是物体由于地球的吸引而受到的力，你要产生这么大的一个重力，就必须把地球当作一个物体，另外用一个地球来吸引它，而这个地球到哪儿去找呢？

“功的原理”告诉我们，任何一种机器，假如在力上占了便宜， 在位置移动的距离上就一定要吃亏。 阿基米德的豪言壮语虽然无法实现，但他生动形象的说明了杠杆能省力， 能够激发学生学习杠杆的爱好。

电热器烧水时间的一个结论及拓展

题目：有甲乙两电热器阻值分别为R1、R2，用甲电热器烧开一壶水需用t1分钟，用乙电热器烧开同一壶水需用t2分钟，若将两电热器分别串联、并联起来，接在同一电源上使用，烧开同样的一壶水所用的时间各是多少分钟(不计热损失)。

分析：此题中隐含的条件为烧开一壶水所吸收的热量相同，即Q甲=Q乙=Q甲乙串=Q甲乙并。

(1)甲乙两电热器单独使用时：

Q甲放=U2t甲/R甲 ①

Q乙放=U2t乙/R乙 ②

(2)甲乙两电热器串联起来使用时：

Q串放=U2t串/R串=U2t串/(R甲 R乙) ③

(3)甲、乙两电热器并联起来使用时：

Q并放=U2t并/R并 ④

R并= R甲·R乙 / R甲 R乙⑤

联立①②③，可得t串=t甲 t乙

联立①②④⑤，可得1/t并=1/t甲 1/t乙

结论：烧开一定质量的水，甲、乙两电热器串联起来使用时所用总时间等于各电热器单独使用时所需时间之和; 甲乙两电热器并联使用时所需时间的倒数等于各电热器单独使用时所需时间的倒数之和。

拓展：若几个电热器串联、并联使用，

则t串=t1 t2 …… tn.

1/t并=1/t1 1/t2…… 1/tn

亲爱的读者，你能自行证实吗？