|
一、选择题:(本大题共12小题. 每小题5分,共60分.)
1.满足条件{0,1}∪A={0,1}的所有集合A的个数是 ( )
A.1个 B. 2个 C. 3个 D.4个
2.某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程. 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是 ( )
3.某工厂去年12月份的产值是去年1月份产值的m倍,则该厂去年产值的月平均增长率为 ( )
4、设U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(C UA) 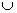 (CUB)= (CUB)=A. {0} B.{0,1} C.{0,1,4} D.{0,1,2,3,4}
5、已知集合A=R,B=R +,若 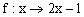 是从集合A到B的一个映射,则B 中的元素3对应A中对应的元素为 A. 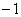 B.1 C.2 D.3 6、设A={(x,y)| y=-4x+6},B={(x,y)| y=5x-3},则A∩B=
A.{1,2} B.{(1,2)} C.{x=1,y=2} D.(1,2)
7、幂函数 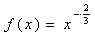 的定义域是 8、已知?( 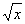 +1)=x+1,则函数?(x)的解析式为 +1)=x+1,则函数?(x)的解析式为A.?(x)=x2 B.?(x)=x2+1 C.?(x)=x2-2x+2 D.?(x)=x2-2x
9、函数y=x2+x (-1≤x≤3 )的值域是
10、已知a>1,函数 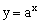 与 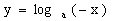 的图像只可能是
11、若 奇函数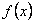 在 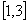 上为 增函数,且有最小值7,则它在  上 A.是减函数,有最小值-7 B.是增函数,有最小值-7
C.是减函数,有最大值-7 D.是增函数,有最大值-7
12、设偶函数 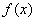 的定义域为 R,当 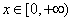 时, 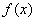 是增函数,则 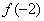 ,  , 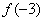 的大小关系是 A. 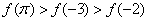 B. 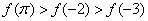 C. 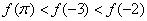 D. 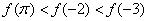 二、填空题:(共6小题.每小题4分,共24分)
13.用集合分别表示下列各图中的阴影部分:
(1) (2) (3) (4)
14、式子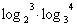 值是______________; 值是______________;
17、函数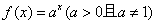 在 在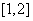 上最大值比最小值大 上最大值比最小值大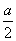 ,则 ,则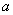 的值为 . 的值为 .
18、王老师给出一个函数 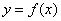 ,四个学生甲、乙、丙、丁各指出了这个函数的一个性质. 甲:对于 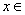 R R,都有 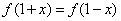 ; 乙: 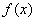 在 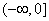 上是减函数; 丙: 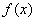 在 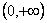 上是增函数; 丁: 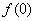 不是函数的最小值. 现已知其中恰有三个说得正确,则这个函数可能是 (只需写出一个这样的函数即可).
三、解答题:(共5小题,共66分)
19.(12分)设x1,x2是关于x的一元二次方程x2-2(m-1)x+m+1=0的两个实根,又y=x21+x22,求y=f(m)的解析式及此函数的定义域.
20、已知集合A={x|x2+ax+b=0},B={1,3},若A=B,求a+b的值;
21、(1)解方程:lg(x+1)+lg(x-2)=lg4 ; (2)解不等式: 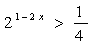 ; ;
22、若0≤x≤2,求函数y= 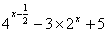 的最大值和最小值; 的最大值和最小值;
23、某商品在近30天内,每件的销售价格P(元)与时间t(天)的函数关系是:
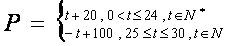 ,该商品的日销售量Q(件)与时间(天)的函数关系是Q= - t+40 (0<t≤30, 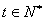 ),求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天? ),求这种商品日销售金额的最大值,并指出日销售金额最大的一天是30天中的哪一天?参考答案
一、选择题:(本大题共12小题. 每小题5分,共60分.)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
D |
B |
D |
C |
C |
B |
B |
C |
B |
B |
D |
A |
二、填空题:(共6小题.每小题4分,共24分)
13、 (1)(A∩C)∪(B∩C)(或(A∪B)∩C);(2)(A∩C)∪B(或(A∪B)∩(C∪B));(3)(A∩CUB)∪(B∩C);(4)A∪(B∩C); 14、2; 15、4; 16、 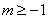 ; 17、 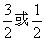 18、 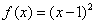 三、解答题:(共5小题,共66分)
19、解:∵x1,x2是x2-2(m-1)x+m+1=0的两个实根,
∴  =4(m-1)2-4(m+1) =4(m-1)2-4(m+1)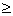 0,解得m 0,解得m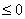 或m 或m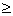 3。 3。
又∵x1+x2=2(m-1), x1·x2=m+1,
∴y=f(m)=x12+x22=(x1+x2)2-2x1x2=4m2-10m+2,
即y=f(m)=4m2-10m+2(m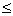 0或m 0或m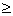 3)。 3)。
20、 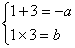 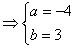 21、解:1)原方程可化为 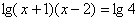 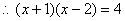 解得x=-2或3
经检验,方程的根为3
2)
22、解: 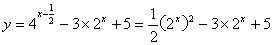 令 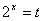
当 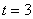 时, 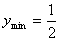
当 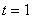 时, 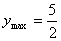
23、解:设日销售额为y元,则

|