一、选择题(以下每题的四个选择支中,仅有一个是正确的)
1、用清水投洗衣服,若每次能洗去污垢的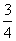 ,要使存留的污垢不超过1%,则至少要投洗的次数是( )
,要使存留的污垢不超过1%,则至少要投洗的次数是( )
(A)3 (B)4 (C)5 (D)6
2、如图,在一根长11cm,外圆周长6cm的圆柱形柱体外表面,用一根细铁丝缠绕,组成10个螺旋,如果铁丝的两端恰好落在圆柱的同一条母线上,则铁丝长度的最小值为( )cm
3、已知锐角α终边上一点的坐标为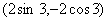 ,则α=( )
,则α=( )
(A)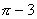 (B)3
(B)3
(C)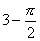 (D)
(D)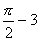
4、区间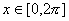 上的函数
上的函数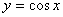 与
与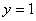 的图象围成的封闭的平面图形的面积为( )
的图象围成的封闭的平面图形的面积为( )
(A)2 (B)4π
(C)2π (D)π
5、已知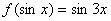 ,则
,则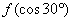 的值为( )
的值为( )
(A)0 (B)1
(C)-1 (D)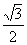
6、一个半径为R的球,在一个内半径也为R的半圆柱形槽内恰好可以无滑动地滚动一周,设球的表面积为S,槽的内壁面积为S′,则S与S′的大小关系是( )
(A)S=S′ (B)S<S′
(C)S>S′ (D)不能确定的
7、设 ,且
,且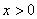 ,则
,则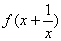 的单调减区间是( )
的单调减区间是( )
(A)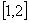 (B)
(B)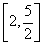
(C)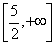 (D)
(D)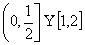
|
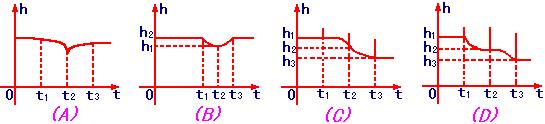
8、如图:在一个盛了水的圆柱形容器内的水面以下有一个用细绳吊着的
下端开了一个很小的孔的充满水的薄壁小球, 当慢慢地匀速地将小球从
水下向水面以上拉动时,柱形容器内水面的高度h与时间t的函数图象大
至是( ) |
9、从集合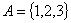 到集合
到集合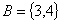 的映射
的映射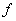 中满足条件
中满足条件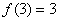 的映射的个数是( )
的映射的个数是( )
(A)2 (B)3
(C)4 (D)5
10、由等式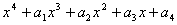
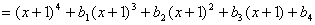 ,定义映射
,定义映射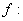
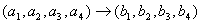 ,则
,则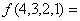 ( )
( )
(A)(1,2,3,4) (B)(0,3,4,0)
(C)(-1,0,2,-2) (D)(0,-3,4,-1)
11、函数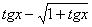 的最小值是( )
的最小值是( )
(A)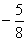 (B)
(B)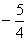
(C)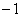 (D)
(D)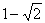
12、函数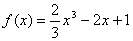 在区间
在区间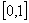 上是( )函数
上是( )函数
(A)单调增加的 (B)单调减少的
(C)先减后增的 (D)先增后减的
13、将抛物线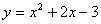 上的各点向右移2单位,再下移1单位,而后将各点横坐标变为原来的
上的各点向右移2单位,再下移1单位,而后将各点横坐标变为原来的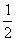 ,则此时的曲线表示的函数是y=( )
,则此时的曲线表示的函数是y=( )
(A)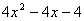 (B)
(B)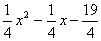
(C)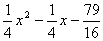 (D)
(D)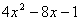
14、若方程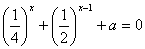 有正数解,则实数
有正数解,则实数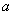 的取值范围是( )
的取值范围是( )
(A)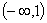 (B)
(B)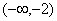
(C)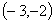 (D)
(D)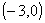
15、若集合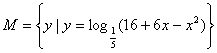 ,
,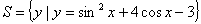
则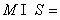 ( )
( )
(A)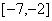 (B)
(B)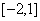
(C)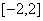 (D)
(D)
16、已知集合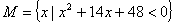 ,
,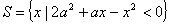 ,
,
若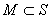 ,则实数
,则实数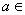 ( )
( )
(A)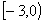 (B)
(B)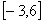
(C)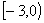
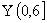 (D)
(D)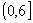
17、若集合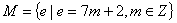 ,
,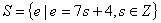
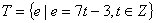 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
(A)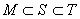 (B)
(B)
(C)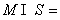 φ,
φ,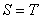 (D)
(D)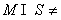 φ,
φ,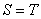
18、平面直角坐标系内,一个圆心在(a, b)的圆包含原点(0, 0),设此圆在第1象限及第3象限的面积和为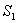 ,在第2象限及第4象限的面积和为
,在第2象限及第4象限的面积和为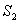 ,则
,则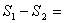 ( )
( )
(A)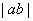 (B)
(B)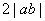 (C)
(C)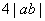
(D)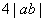 (当
(当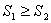 时),或
时),或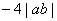 (当
(当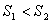 时)
时)
19、函数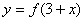 与
与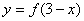 的图象是( )
的图象是( )
(A)关于直线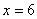 对称 (B)关于直线
对称 (B)关于直线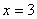 对称
对称
(C)关于直线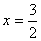 对称 (D)关于y轴对称
对称 (D)关于y轴对称
20、四棱锥的四个侧面中,互相垂直的平面对至多有( )
(A)1对 (B)2对
(C)3对 (D)4对
21、已知函数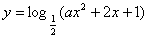 的值域为R,则实数a的取值范围是( )
的值域为R,则实数a的取值范围是( )
(A)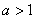 (B)
(B)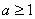
(C)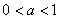 (D)
(D)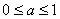
22、关于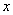 的方程,
的方程,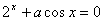 恰有一个实根,则实数a的值是( )
恰有一个实根,则实数a的值是( )
(A)1 (B)-1
(C)-2 (D)不确定的
23、正方形ABCD的一边AB在平面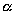 内,AC与
内,AC与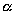 成30°角,则AD与
成30°角,则AD与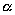 所成的角等于( )
所成的角等于( )
(A)60° (B)75°
(C)45° (D)30°
24、已知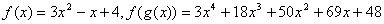 ,那么
,那么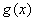 的各项系数和为( )
的各项系数和为( )
(A)8 (B)9
(C)10 (D)11
25、某工厂三年内产值持续增长,三年的年增长率分别为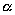 、
、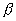 、
、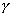 ,则这三年的平均年增长率为( )
,则这三年的平均年增长率为( )
(A)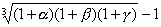 (B)
(B)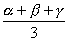
(C)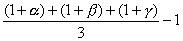 (D)
(D)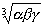
二、填空题
26、若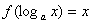 ,那么
,那么 ( )
( )
27、若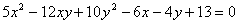 ,则
,则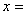 ( ),
( ),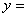 ( )
( )
28、方程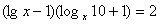 的解是( )
的解是( )
29、正四面体(四个面都是正三角形的四面体)的棱长为a,以面三角形的重心的连结线段为边构成的四面体的体积是( )
30、在六面体ABCDE中,D-ABC和E-ABC都是正四面体,则棱AD和棱BE所成锐角的余弦值是( )
31、方程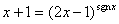 的解是( ),其中符号函数
的解是( ),其中符号函数
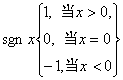
32、若方程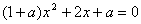 的根是正数,则参数a的取值范围是( )
的根是正数,则参数a的取值范围是( )
33、正三棱锥A-BCD的侧棱长与底面边长相等,顶点A、B、C、D在同一个球面上,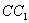 和
和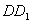 是该球的直径,则平面ABC与平面
是该球的直径,则平面ABC与平面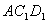 所成角的正弦值为( )
所成角的正弦值为( )
34、函数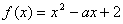 对于任意的
对于任意的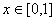 ,都有
,都有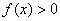 ,则实数a的取值范围是( )
,则实数a的取值范围是( )
35、偶函数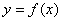 的定义域为R,且对于任意
的定义域为R,且对于任意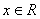 ,都有
,都有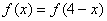 ,又当
,又当
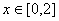 时,
时,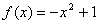 ,则当
,则当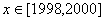 时,
时,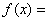 ( )
( )
36、A、B、C是同一条直线上的三点,AB=BC=1千米,塔M在A的正东北方向,在B的正东方向,在C的南偏东60°,则塔与直线AC的距离等于( )
37、集合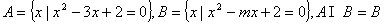 ,则实数m的取值范围是( )
,则实数m的取值范围是( )
38、正三棱锥V-ABC底面边长及锥高都等于4,过AB的截面将棱锥体积二等分,则锥顶V到该截面的距离等于( )
39、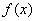 是定义在R上的偶函数,且是周期为2的周期函数,当
是定义在R上的偶函数,且是周期为2的周期函数,当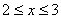 时,
时,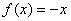 ,则
,则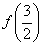 的值为( )
的值为( )
40、在集合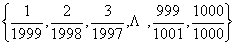 中,有既约分数( )个
中,有既约分数( )个
41、函数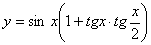 的最小正周期是( )
的最小正周期是( )
42、函数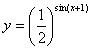 的单调减区间是( )
的单调减区间是( )
43、函数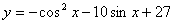 的最大值为( ),最小值为( )
的最大值为( ),最小值为( )
44、若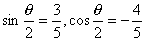 ,则
,则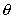 的终边在( )象限
的终边在( )象限
45、方程 在
在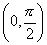 上有解,则a的取值范围是( )
上有解,则a的取值范围是( )
46、中午12时以后时针与分针第一次重合的时间是13时( )分
47、设d是任意四面体的相对棱之间距离的最小值,h是四面体最小高的长度,
则2d( )h。(填<、>或=)
48、设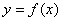 是定义在R上的函数,且对于任意实数a,b,有
是定义在R上的函数,且对于任意实数a,b,有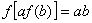 ,
,
则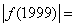 ( )
( )
49、方程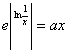 有定,则a的取值范围是( )
有定,则a的取值范围是( )
50、当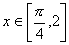 时,
时,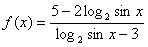 的值域是( )
的值域是( )
51、若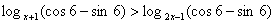 ,则x的取值范围是( )
,则x的取值范围是( )
52、二次函数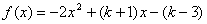 与x轴有两个交点,且这两个交点的距离大于1,则k的取值范围是( )
与x轴有两个交点,且这两个交点的距离大于1,则k的取值范围是( )
53、如果正四面体的内切球的体积是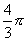 ,那么正四面体的体积是( )
,那么正四面体的体积是( )
54、已知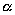 、
、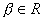 且
且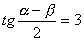 ,则乘积
,则乘积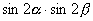 的最大值为( )
的最大值为( )
55、已知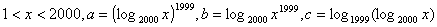 ,则a,b,c由小到大的顺序是( )
,则a,b,c由小到大的顺序是( )
56、函数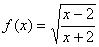 的定义域为集合A,函数
的定义域为集合A,函数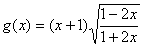 的定义域为集合B,则
的定义域为集合B,则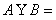 ( )
( )
57、定义在R上的函数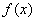 满足
满足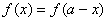 ,(a是大于1的整数),若方程
,(a是大于1的整数),若方程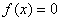 有n个实根,它们的和为2001,则a、n的值可能有( )种
有n个实根,它们的和为2001,则a、n的值可能有( )种
58、若方程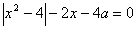 恰有两个不同的实数根,则实数a的取值范围是( )
恰有两个不同的实数根,则实数a的取值范围是( )
59、半径为R的球的内接正四面体的体积等于( )
60、在△ABC中,CD⊥AB于D,且AD·BC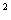 +BD·AC
+BD·AC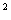 =2AC·BC·CD,
=2AC·BC·CD,
则∠ACB=( )
61、计算并观察: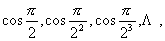 归纳得到
归纳得到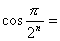 ( )
( )
|
62、如图:从正方体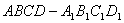 的棱AB的顶点A出发, 的棱AB的顶点A出发,
沿正方体的棱到达另一顶点B,若经过一个顶点的次数不超过1,
则不同的道路共有( )条。 |
|
63、如图所示:SA和SB分别是由点光源S射向两个平面镜的光线,
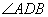 是对应的两条法线的夹角, 是对应的两条法线的夹角,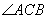 是两条反射光线的夹角, 是两条反射光线的夹角,
则∠S,∠D,∠A之间的关系是( ) |
64、对于实数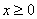 ,定义符号
,定义符号 表示不超过x的最大(正)整数,
表示不超过x的最大(正)整数,
则方程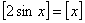 的解集(x以弧度为单位)是( )
的解集(x以弧度为单位)是( )
65、函数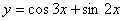 的最小正周期是( )
的最小正周期是( )
66、适合方程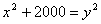 的正整数解有( )组
的正整数解有( )组
67、设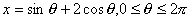 ,则函数
,则函数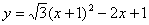 的最小值是( ),最大值是( )
的最小值是( ),最大值是( )
68、已知函数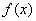 的值域是
的值域是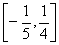 ,则函数
,则函数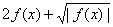 的值域是( )
的值域是( )
69、函数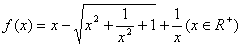 的最大值是( )
的最大值是( )
|
70、一块长方形木料,
按图中所示的余弦线截去一块,
则剩余部分的体积是( )
|
71、若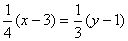 ,则
,则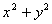 的最小值是( )
的最小值是( )
|
72、在越野比赛中,摩托车要经过如图所示的30°的斜坡
AB,再越过10米宽的壕沟CD,降到落差5米的平路DE
上继续行驶,则摩托车从B点驶出时的速度至少是( )
米/秒。(取重力加速度g=10米/秒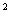 ) ) |
73、不等式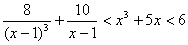 的解是( )
的解是( )
74、关于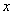 的方程
的方程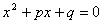 的两个根是两个连续整数,q是质数,则p的值是( )
的两个根是两个连续整数,q是质数,则p的值是( )
75、函数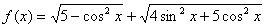 的最大值是( ),最小值是( )
的最大值是( ),最小值是( )
三、解答题
76、已知函数关系式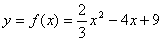 ,
,
(1)当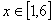 时,求
时,求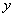 的值域;
的值域;
(2)求实数m、n,使得当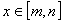 时,
时,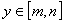
77、设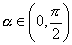 ,函数
,函数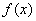 的定义域为[0,1]且
的定义域为[0,1]且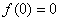 ,
,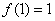 ,当
,当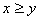 时,
时,
有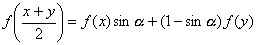 ,求
,求
(1)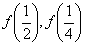 ;
;
(2)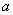 的值;
的值;
(3)函数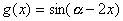 的单调递增区间。
的单调递增区间。
|
79、如图所示:矩形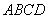 中, 中,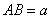 , ,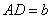 ,P为CD上 ,P为CD上
的任意一点,以AB所在直线为轴,将△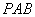 旋转而成一个旋转 旋转而成一个旋转
体,求旋转体表面积的最大值,并指出当表面积最大时P点位置。 |
|
80、在一张半径为2米的水平圆桌正中央上空挂一盏电灯,已知桌子边缘一点处的亮度为E,灯光射到桌子边缘的光线与桌面的夹角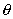 及这一点到光源的距离 及这一点到光源的距离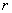 三者之间的关系为: 三者之间的关系为:
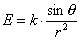 (其中k是一个与电灯光的强度有关的常数), (其中k是一个与电灯光的强度有关的常数),
问要使桌子边缘处最亮,求电灯悬挂的高度h。 |