时间:120分钟 满分:150分 考试时间:2001年7月 命题人:李德胜
第Ⅰ卷 (选择题 共60分)
一、选择题:(本大题共12小题,每题5分,共计60分,在每题给出的四个选项中,只有一个是正确的)
1.已知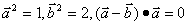 ,则
,则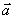 与
与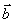 的夹角是 ( )
的夹角是 ( )
(A)60° (B) 90° (C) 45° (D) 30°
2.函数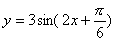 的图象是轴对称图形,它的一条对称轴是 ( )
的图象是轴对称图形,它的一条对称轴是 ( )
(A)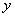 轴 (B)直线
轴 (B)直线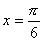 (C)直线
(C)直线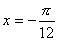 (D)直线
(D)直线
3.函数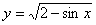 的值域是 ( )
的值域是 ( )
(A)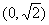 (B)
(B) 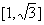 (C)
(C) 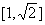 (D)
(D) 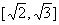
4.将函数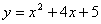 的图象按向量
的图象按向量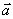 经过一次平移后,得到
经过一次平移后,得到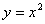 的图象,则向量
的图象,则向量
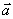 等于( )
等于( )
(A)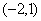 (B)
(B)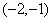 (C)
(C) 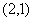 (D)
(D)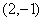
5.使函数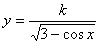 取得最小值1时的
取得最小值1时的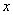 恰使函数
恰使函数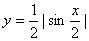 取得最大值,则
取得最大值,则
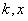 分别为( )
分别为( )
(A)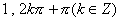 (B)
(B)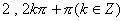
(C)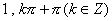 (D)
(D)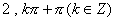
6.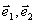 是表示平面内所有向量的一组基底,则下面四组向量中,不能作为一组基底的
是表示平面内所有向量的一组基底,则下面四组向量中,不能作为一组基底的
是 ( )
(A)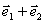 和
和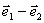 (B)
(B)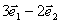 和
和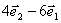
(C)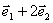 和
和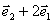 (D)
(D)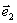 和
和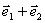
7.已知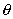 是三角形的一个内角,函数
是三角形的一个内角,函数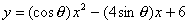 对一切
对一切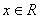 恒取正
恒取正
值,则角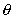 的取值范围是 ( )
的取值范围是 ( )
(A)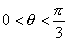 (B)
(B)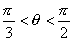 (C)
(C) 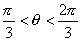 (D)
(D)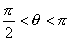
8.已知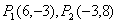 ,且
,且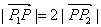 ,点
,点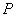 在线段
在线段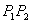 的延长线上,则
的延长线上,则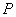 点的
点的
坐标为 ( )
(A)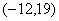 (B)
(B)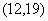 (C)
(C) 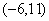 (D)
(D)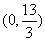
9.下列函数中,最小正周期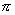 为的偶函数是 ( )
为的偶函数是 ( )
(A)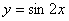 (B)
(B)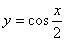 (C)
(C)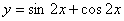 (D)
(D)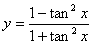
10.在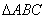 中,已知
中,已知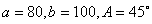 ,则此三角形有 ( )
,则此三角形有 ( )
(A) 一解 (B)两解 (C) 一解或两解 (D) 无解
11.函数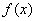 是以4为周期的奇函数,且
是以4为周期的奇函数,且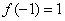 ,则
,则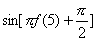 的值为( )
的值为( )
(A) 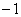 (B)0 (C)
(B)0 (C)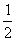 (D)1
(D)1
12.函数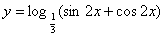 的单调递减区间是 ( )
的单调递减区间是 ( )
(A)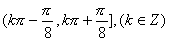 (B)
(B) 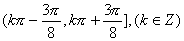
(C)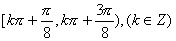 (D)
(D)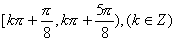
第Ⅱ卷 (非选择题 共90分)
二、填空题:(本大题共4小题,每题4分,共16分)
13.已知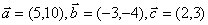 ,且
,且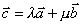 ,则
,则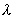 = ;
= ;
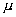 = 。
= 。
14.若函数y=3cos(ωx+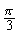 )的周期为T,且T∈(2,3),则正整数ω是________。
)的周期为T,且T∈(2,3),则正整数ω是________。
15.已知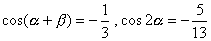 ,
,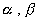 均为钝角,那么
均为钝角,那么
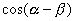 = 。
= 。
16.设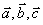 是任意的非零平面向量,且相互不共线,则:
是任意的非零平面向量,且相互不共线,则:
①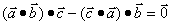 ;
;
②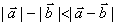 ;
;
③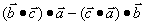 不与
不与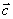 垂直;
垂直;
④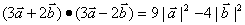
把你认为正确的命题的序号都填在横线上 。
三、解答题:(本大题共6小题,计76分)
17.(本小题满分12分)
已知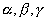 都是锐角,且
都是锐角,且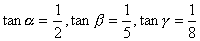 ,求
,求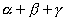 的值。
的值。
18.(本小题满分12分)
已知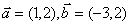 ,当k为何值时,
,当k为何值时,
(1)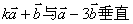 ?
?
(2)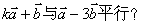 平行时它们是同向还是反向?
平行时它们是同向还是反向?
 19.(本小题满分12分)
19.(本小题满分12分)
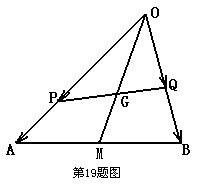
如右图,PQ过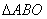 重心G,
重心G,
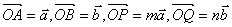 ,
,
求证: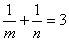
20.(本小题满分12分)
在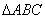 中,设
中,设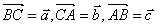 ,证明
,证明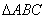 为正三角形的充要条件是
为正三角形的充要条件是
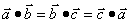
21.(本小题满分12分)
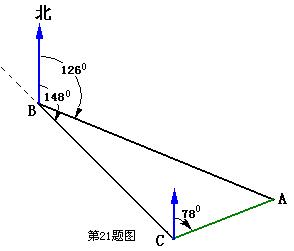
 如图,货轮在海上航行以35 n mile/h的速
如图,货轮在海上航行以35 n mile/h的速
度沿着方位角(从指北方向顺时针转到目
标方向线的水平角)为148°的方向航行。
为了确定船位,在B点观测灯塔A的方
位角是126°,航行半小时后到达C点,
观测灯塔A的方位角是78°,求货轮到
达C点时与灯塔A的距离
(精确到1 n mile)
(可能用到的数据:
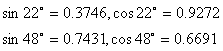 )
)
22.(本小题满分14分)
若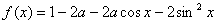 的最小值为
的最小值为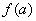
(1)用 表示
表示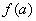 的表达式;
的表达式;
(2)求能使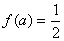 的
的 的值,并求出当
的值,并求出当 取此值时
取此值时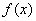 的最大值。
的最大值。
2000——2001学年度高一第二学期期末考试
数学答题卡 2001、7
一、选择题(本大题共12小题,每题5分,共计60分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题:(本大题共4小题,每题4分,共16分)
13 ; ; 14 ;
15 ; 16 。
三、解答题:
17.(本小题满分12分)
解:
18.(本小题满分12分)
解:
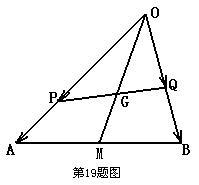 19.(本小题满分12分)
19.(本小题满分12分)
证明:
20.(本小题满分12分)
证明:
21.(本小题满分12分)
 解:
解:
22.(本小题满分14分)
解: