巧求图形的周长

正方形周长＝边长×4，长方形周长＝（长＋宽）×2＝长×2＋宽×2

这两个计算公式看起来十分简单，但用途却十分广泛。利用它们可以巧求一些复杂图形的周长。解决这类问题主要从两方面入手：

1、对于一些运用拼和剪来构造新图形的问题，我们经常要画图帮助理解，仔细分析，思考怎样从已知条件中找到求周长所要的条件或找到新图形周长与原来图形周长间的关系，再求出它的周长。

2、对于一些不规则的比较复杂的图形，求它们的周长，往往要运用“平移、转化”等方法把问题转化成长方形或正方形的周长。在转化过程中要抓住“变”与“不变”两个部分，而且不能遗漏掉某些线段的长度。

例1、用3个周长是15厘米的正方形拼成一个长方形，求所拼成的长方形的周长。

分析与解答：请你画图后再思考解答。

试一试1、用3个周长是17厘米的正方形拼成一个长方形，求所拼成的长方形的周长。

例2、一张长方形纸长是32厘米，宽20厘米，先剪下一个最大的正方形纸片，再从余下的纸片中又剪下一个最大的正方形，最后剩下的长方形纸片的周长是多少厘米？

分析与解答：先画图，然后想一想，第一次剪的正方形的边长是多少，第二次剪的正方形的边长是多少。

试一试2、在一个长是24厘米，宽15厘米长方形纸中，先剪下一个最大的正方形纸片，再从余下的纸片中又剪下一个最大的正方形，最后剩下的长方形纸片的周长是多少厘米？

例3、计算下列图形（左图）的周长(单位：厘米)。

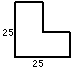
分析与解答：将图中右上缺角处的线段分别向上、向右平行移动，这样正好移补成一个正方形。

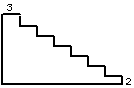
试一试3、如上右图是一个楼梯的侧剖图。已知每步台阶宽3分米，高2分米。求这个楼梯侧面的周长是多少米？

例4、求下面图（1）的周长(单位：厘米)。

分析与解答：求这个图形的周长，我们也同样采用转化的方法，想一想，可以转化成什么图形，转化后图形的周长与原来图形周长之间有什么样的关系，可以怎样求原图的周长。

试一试4、求上图（2）的周长。

例5、用长9厘米、宽5厘米的长方形摆成下图外形，最上层是一个长方形，以下每层多一个长方形，得到的图形的周长是多少厘米？

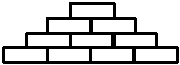
分析与解答：想一想、画一画，可以将原图转化成什么样的图形，怎样求转化后的图形的周长，必须要知道什么条件？

试一试5、若按上面的摆法，摆10层，它的周长是多少呢？

例6、下图（左）是一个方形螺线。已知两相邻平行线之间的距离均为1 厘米，

求螺线的总长度。

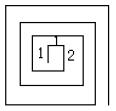
分析与解答：如上（中）图所示，按箭头方向转动虚线部分，于是得到了三个边长分别为3，5，7 厘米的正方形和中间一个三边图形(见上右图)。所以螺线总长度为

试一试6、右图两相邻的平行线之间距离为2厘米，求它的周长。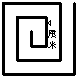

练习：

1、用3个边长是3厘米的正方形拼成一个长方形，求所拼成的长方形的周长。

2、一个长方形长60厘米，宽20厘米，将它剪成3个正方形，每个正方形的周长是多少？

3、四个周长为17厘米的长方形拼成一个大长方形，求大长方形的周长。（下图1）

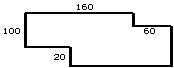
4、上图（2）是一公园的平面图，王奶奶天天早晨绕它跑3圈，王奶奶天天早晨跑多少米？（上右图）

5、上图（3）是一个“I”字形大楼平面图，请求出它的周长。（单位：米）　　　　　　　　　　　　　　

6、如上图（4）所示，一个正方形被分成了三个相同的长方形。假如其中一个长方形的周长是16 米，那么这个正方形的周长是多少米？