|
有经验的渔民,在叉鱼时,不是对准看到的鱼,而是对准所见鱼的下方,这是由于光在界面上的折射使得鱼在水中的视位置比实际位置升高的缘故。
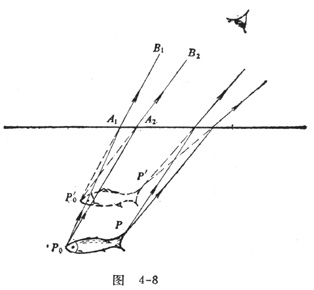
我们先作一下定性解释。如图4-8所示,从鱼头P0发出的光线P0A1、P2A2分别在水和空气的界面A1、A2处发生折射,沿A1B1、A2B2方向进入眼睛,由于人眼在直觉上总是认为光是沿直线射来的,所以人觉得折射光线A1B1、A2B2是从它们延长线的交点P0′射来的,P0′就是眼睛看到的P0的像。同理眼睛看到的P点的像在P′处。鱼的视位置比鱼的实际位置升高了。
如果我们作一些定量分析,还可以发现不仅鱼的位置升高了,而且由于光折射的结果,产生了像散,像的清晰度也由于像散而受到破坏。
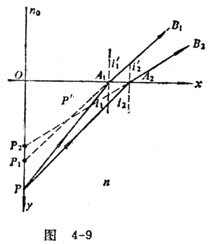
如图4-9所示,我们选OX轴为空气和水的分界面,n为水的折射率,n0为空气的折射率。鱼身上的某点P为发光点,以OP为y轴,则P点的坐标为(0,y)。PA1、PA2为P发射的单心光束中两条靠得很近的光线,入射点A1、A2的坐标为(x1,0)、(x2,0)。入射角为i1和i2,折射角为i1′和i2′。折射线A1B1、A2B2向后延长分别交y轴于P1(0,y1)、P2(0,y2),并且它们在图平面内相交于P′点。
由图中三角形POA1,POA2得:
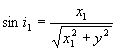
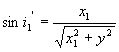
代入折射定律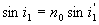 ,并解出y1,则有 ,并解出y1,则有
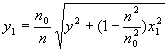
用同样的方法可以求出y2有类似的形式。
同样我们也可以计算出A1B1、A2B2两条折射线的交点P′的坐标(x′,y′)分别为
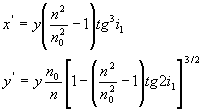
因为n>n0,所以x′>0,即P′点在oy轴的右边。
现让我们回过头来分析(2)式。由(2)式可知,当P的位置一定时(y不变),P1点的位置(O,y1)将随入射点A1的位置(x1,0)的不同而变,在式中,因为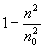 是负的,故x1越大,y1越小,即入射点离Oy轴越远,P1点离Ox轴越近。由此可知,A1B1与A2B2的交点产P′必在Oy轴之右。从P点发出的并位于PA1与PA2之间的所有光线的折射线延长后都交于P′点附近,而与Oy轴交于P1和P2两点之间。P1、P2、P′三点不重合,这说明从P点发出的单心光束,经水面折射后变成了像散光束。只有当P发出的光束几乎垂直于界面时(i1=0),P1、P2、P′三点才几乎重合,即在水面上沿竖直方向向下观看水中鱼时,所见像是清晰的,此时像的深度y′称为像似深度, 是负的,故x1越大,y1越小,即入射点离Oy轴越远,P1点离Ox轴越近。由此可知,A1B1与A2B2的交点产P′必在Oy轴之右。从P点发出的并位于PA1与PA2之间的所有光线的折射线延长后都交于P′点附近,而与Oy轴交于P1和P2两点之间。P1、P2、P′三点不重合,这说明从P点发出的单心光束,经水面折射后变成了像散光束。只有当P发出的光束几乎垂直于界面时(i1=0),P1、P2、P′三点才几乎重合,即在水面上沿竖直方向向下观看水中鱼时,所见像是清晰的,此时像的深度y′称为像似深度,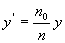 。因为n>n0,所以鱼的像似深度,总是小于鱼的实际深度。而入射光的方向越倾斜,折射光束像散就越显著,也就是说,在沿着倾斜角度较大的方向观看鱼时,鱼的像不仅由于折射而上升。而且清晰度也由于像散而受到破坏,人们看到的将是一个模糊的,比实际位置上升的虚像。 。因为n>n0,所以鱼的像似深度,总是小于鱼的实际深度。而入射光的方向越倾斜,折射光束像散就越显著,也就是说,在沿着倾斜角度较大的方向观看鱼时,鱼的像不仅由于折射而上升。而且清晰度也由于像散而受到破坏,人们看到的将是一个模糊的,比实际位置上升的虚像。
|