| |
|
[组图]数学史上的一场论战
|
|
中世纪的欧洲,代数学的发展几乎处于停滞的状态,其真正的起步,始于公元1535年的一场震动数学界的论战.
大家知道,尽管在古代的巴比伦或古代的中国,都已掌握了某些类型一元二次方程解法.但一元二次方程的公式解法,却是由中亚数学家阿尔·花拉子米于公元825年给出的.花拉子米是把方程
x2+px+q=0
配方后改写为
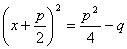
的形式,从而得出了方程的两个根为
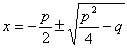
在欧洲,被誉为“代数学鼻祖”的古希腊的丢番图,虽然也曾得到过类似的式子,但由于丢番图认定只有根式下的数是一个完全平方数,且根为正数时,方程才算有解,因而数学史上都认为阿尔·花拉子米为求得一元二次方程一般解的第一人.
花拉子米之后,许多数学家都致力于三次方程公式解的探求,但在数百年漫漫的历史长河中,除了取得个别方程的特解外,都没有人取得实质性进展,许多人因此怀疑这样的公式解根本不存在!
话说当时意大利的波伦亚大学,有一位叫费洛的数学教授,也潜心于三次方程公式解这一当时世界难题的研究,功夫不负有心人,他终于取得了重大突破.公元1505年,费洛宣布自己已经找到了形如
x3+px=q
方程的一个特别情形的解法,但他没有公开自己的成果,为的是能在一次国际性的数学竞赛中一放光彩.遗憾的是,费洛没能等到一个显示自己的才华的机会就抱恨逝去,临死前他把自己的方法传给了得意门生,威尼斯的佛罗雷都斯.
现在话转另外一头,在意大利北部的布里西亚,有一个颇有名气的年轻人,叫塔塔里亚(Nicolo Tartaglia,1500-1557),此人从小天资聪明,勤奋好学,在数学方面表现出超人的才华,尤其是他发表的一些论文,思路奇特,见地高远,因而一时间名闻遐迩.
塔塔里亚自学成才自然受到了当时一些习惯势力的歧视,公元1530年,当时布里西亚的一些人公开向塔塔里亚发难,提出以下两道具有挑战性的问题:
(1)求一个数,其立方加上平方的3倍等于5;
(2)求三个数,其中第二个数比第一个数大2,第三个数又比第二个数大2,它们的积为1000.
读者不难知道,对第一个问题,若令所求数为x,则依题意有:
x3+3x2=5
而对第二个问题,令第一个数为x,则第二、三数分别为x+2,x+4,于是依题意有:
x(x+2)(x+4)=1000
化简后
x3+6x2+8x-1000=0
以上是两道三次方程的求解问题,塔塔里亚求出了这两道方程的 [1] [2] 下一页
|
来源:中国哲士网
世界人物库,古今中外人物资料 塔塔里亚简介,介绍,生平事迹 图片照片
有关作品[组图]数学史上的一场论战详细资料
|
| 上一篇文章: 塔塔里亚生平介绍 |
| 下一篇文章: 没有了 |
| |
|
|