达朗贝尔惯性力的概念
在研究刚体在非惯性基下的运动规律时引入了惯性力的概念。本节将定义另一种惯性力。
考虑在惯性基下质点的运动。根据牛顿定律,该质点的动力学方程为
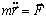
|
(7.1-1) |
如果定义
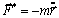
|
(7.1-2) |
为该质点的达朗贝尔惯性力,那么动力学方程(7.1-1)可表为
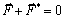
|
(7.1-3) |
由此可得到如下结论:质点运动的任意时刻,质点的达朗贝尔惯性力与作用于质点的所有真实的作用力组成平衡力系。此结论称为质点的达朗贝尔原理。
上述的真实的作用力指作用于质点的外力(包括理想约束力)。需要注意的是,达朗贝尔惯性力与非惯性基下的引进的惯性力是两种意义下的概念,后者是为了使非惯性基下相对运动的动力学方程与在惯性基下的动力学方程形式上相似而定义的惯性力,它与非惯性基运动有关。而这里引入达朗贝尔惯性力是为了将惯性基下的质点动力学方程(7.1-1)变换为一种力的平衡方程(7.1-3)的形式,尽管此时质点并非处在平衡状态。这种处理方法称为动静法。此外达朗贝尔惯性力与质点的绝对加速度有关,与有无非惯性基无关。有时达朗贝尔惯性力也简称为惯性力,读者不难从应用的过程中与非惯性基下的惯性力加以区分。