等。他说的“差率”“变率”就是微分。与此同时，他还在1676年首次公布了他发明的二项式展开定理。牛顿利甩它还发现了其他无穷级数，并用来计算面积、积分、解方程等等。1684年莱布尼兹从对曲线的切线研究中引入了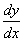
和拉长的S作为微积分符号，从此牛顿创立的微积分学在大陆各国迅速推广。
微积分的出现，成了数学发展中除几何与代数以外的另一重要分支──数学分析（牛顿称之为“借助于无限多项方程的分析”），并进一步进进发展为微分几何、微分方程、变分法等等，这些又反过来促进了理论物理学的发展。例如瑞士J.伯努利曾征求最速降落曲线的解答，这是变分法的最初始问题，半年内全欧数学家无人能解答。1697年，一天牛顿偶然听说此事，当天晚上一举解出，并匿名刊登在《哲学学报》上。伯努利惊异地说：“从这锋利的爪中我认出了雄狮”。
（2）牛顿在光学上的成就
牛顿的《光学》是他的另一本科学经典著作（1704年）。该书用标副标题是“关于光的反射、折射、拐折和颜色的论文”，集中反映了他的光学成就。
第一篇是几何光学和颜色理论（棱镜光谱实验）。从1663年起，他开始磨制透镜和自制望远镜。在他送交皇家学会的信中报告说：“我在1666年初做了一个三角形的玻璃棱镜，以便试验那著名的颜色现象。为此，我弄暗我的房间……”接着详细叙述了他开小孔、引阳光进行的棱镜色散实验。关于光的颜色理论从亚里士多德到笛卡儿都认为白光纯洁均匀，乃是光的本色。“色光乃是白光的变种。牛顿细致地注意到
上一页 [1] [2] [3] [4] [5] [6] [7] 下一页
